Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 35

Um rolo de papel tem um peso uniforme de 3,75   N ( ≈ 0,375   k g ) e está suspenso pela porta-papel de modo que se apoia contra a parede. Se o porta-papel tem um peso desprezível e o rolamento em O pode ser considerado sem atrito, determine a força P necessária para começar a girar o rolo se θ = 30 ° . O coeficiente de atrito estático entre a parede e o papel μ s = 0,25 .

Passo 1

O problema pede que descubra o menor força P para começar a girar o rolo.

Beleza, se a gente analisar cada eixo separadamente, vamos encontrar:

N A - R sen ⁡ 30 ° + P sen ⁡ 30 ° = 0

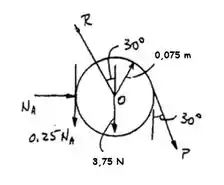
E na vertical agora:

R cos ⁡ 30 ° - 3,75 - P cos ⁡ 30 ° - F a t = 0

R cos ⁡ 30 ° - 3,75 - P cos ⁡ 30 ° - 0,25 N A = 0

Também vamos analisar o momento tendo como eixo o ponto O :

0,25 N A 0,075 - P 0,075 = 0

P = 0,25 N A

Passo 2

Pra encontrar algum dos valores vamos igualar as equações da vertical e horizontal e substituir P :

N A - R sen ⁡ 30 ° + P sen ⁡ 30 ° = R cos ⁡ 30 ° - 3,75 - P cos ⁡ 30 ° - 0,25 N A

N A - R sen ⁡ 30 ° + ( 0,25 N A ) sen ⁡ 30 ° = R cos ⁡ 30 ° - 3,75 - ( 0,25 N A ) cos ⁡ 30 ° - 0,25 N A

N A - 0,5 R + 0,125 N A = 0,866 R - 3,75 - 0,2165 N A - 0,25 N A

1,5915 N A - 1,366 R = 3,75

E a gente monta um sistema com a equação horizontal e substituimos P :

1,5915 N A - 1,366 R = 3,75 N A - R sen ⁡ 30 ° + 0,25 N A sen ⁡ 30 ° = 0

Assim a gente encontra:

N A = 2,53   N

Passo 3

Calma, tá quase acabando, agora a gente calcula P usando o que já temos:

P = 0,25 N A

P = 0,25 2,53

P = 0,6325   N

Resposta

P = 0,6325   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de concreto de 500 N é elevado por um par de pinças mostrado na figura. Determine o menor valor admissível do coeficiente de atrito estático entre o bloco e as pinças em F e G.
Uma escada AB de 6,5 m encosta-se em uma parede como mostrado na figura. Considerando que o coeficiente de atrito estático μ s é o mesmo para A e B, determine o menor valor de μ s para que o equilíbri
Um binário M de intensidade 100 N.m é aplicado ao tambor, tal como mostra a figura. Determine a menor força que deve ser exercida pelo cilindro hidráulico nas uniões B e E para que o tambor não gire.
Uma haste delgada de comprimento L está apoiada entre um pino C e uma parede vertical e sustenta uma carga P em sua extremidade A. Sabendo que o coeficiente de atrito estático é 0,20 em B e C, calcule
Um eixo excêntrico de 100 mm de raio mostrado na figura é usado para controlar o movimento da placa CD. Sabendo que o coeficiente de atrito estático entre o excêntrico e a placa é 0,45, e desprezando