Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 34
Uma viga de 3 m, pesando 5400 N, é movida para a esquerda sobre a plataforma. A força horizontal P é aplicada no carrinho, que é montado em rodas sem atrito. Os coeficientes de atrito entre as superfícies são e , e inicialmente . Sabendo que a superfície superior do carrinho é ligeiramente mais alta que a plataforma, determine a força P necessária para iniciar o movimento da viga (Dica: A viga é suportada em A e D.)
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para a viga:
Sabemos que a força de atrito nos pontos A e D pode ser escrita como:
Passo 2
Agora vamos aplicar o somatório de momento em relação ao ponto A:
Aplicando o somatório de forças na direção :
Dessa forma, podemos calcular as forças de atrito nos pontos A e D:
Como a força de atrito em D é maior do que em A, o escorregamento ocorre primeiro em A, então usando esse valor como restrição e aplicando o somatório de forças na direção :
Passo 3
Agora vamos desenhar o diagrama de corpo livre para o carrinho:
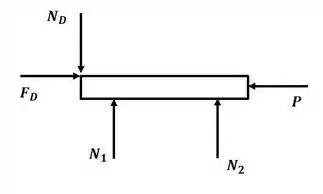
Aplicando o somatório de forças na direção :