Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 40
Duas tábuas uniformes idênticas, cada qual pesando 180 N, estão encostadas temporariamente uma contra a outra tal como mostra a figura. Sabendo que o coeficiente de atrito estático entre todas as superfícies é 0,40, determine a maior intensidade da força para que o equilíbrio seja mantido, a superfície em que o movimento é iminente.
Passo 1
Tá legal! Vamos começar esse excercício assumindo uma tendência de movimento em C, desenhando o DCL para a tábua da direita:
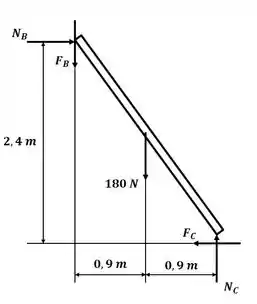
Sabemos que a força de atrito pode ser calculada por:
Agora, aplicando o somatório de momento em relação ao ponto B:
Substituindo esse valor na equação para :
Agora aplicando o somatório de forças na direção :
Agora podemos aplicar o somatório de forças na direção :
Como a força de atrito estático máxima nesse ponto é dada por:
Então, como não há movimento.
Passo 2
Agora vamos desenhar o diagrama de corpo livre para a tábua da esquerda:
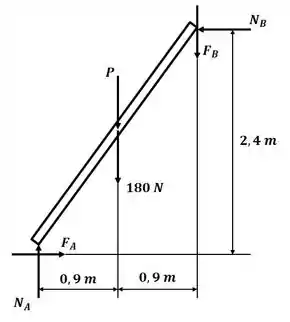
Agora, aplicando o somatório de momento em relação ao ponto A:
Substituindo os valores encontrados para e :
Passo 3
Agora devemos checar se haverá ou não escorregamento no ponto A, para isso, iremos aplicar o somatório de forças na direção para o DCL do passo 2:
Agora aplicando o somatório de forças na direção :
E, a força de atrito máximo será:
Então, como não haverá deslizamento. Então realmente a superfície onde o movimento é iminente é em C.