Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 41

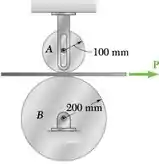
Uma correia de massa desprezível passa entre os cilindros A e B e é puxada para a direita com a força P. Os cilindros A e B têm respectivamente massa de 2,5 e 10 kg. O eixo do cilindro A é livre para deslizar no rasgo vertical e os coeficientes de atrito entre a correia e cada cilindro são μ s = 0.50 e μ k = 0.40 . Para P = 18 N, determine (a) se ocorre ou não deslizamento entre a correia e um dos cilindros, (b) a aceleração angular de cada cilindro.

Passo 1

Suponha que nenhum escorregamento ocorra.

Então:

a cinto = 4   in . α A = 8   in . α B

α B = 1 2 α A

Passo 2

Cilindro A.

+ Σ M G = Σ M G eff :             F A 4 12 ft = I - A α A

F B 4 12 = 1 2 5 g 4 12 2 α A

F A = 5 6 α A g

Passo 3

Cilindro B.

+ Σ M G = Σ M G eff :             F B 8 12 ft = I - B α B

F A 8 12 = 1 2 20 g 8 12 2 1 2 α A

F B = 20 6 α A g

Passo 4

Cinto

→ + Σ F A = 0 :             P - F A - F B = 0

3.60 - 5 6 α A g - 20 6 α A g = 0

α A = 3.60 6 25 g = 0.864   g

α A = 27.82   rad/ s 2  

Passo 5

Verifique se a correia não desliza.

De (2):

F A = 5 6 0.864 = 0.720   lb

De (4):

F e = P - F A = 3.60 - 0.720 = 2.88   lb

Mas

F m = μ s N = 0.50 5   lb = 2.50   lb

Passo 6

Como Fc > Fm, a suposição está errada.

Refazemos a análise de B, assumindo escorregamento.

α B ≠ 1 2 α A

F B = μ k N = 0.40 5   lb = 2   lb

+ Σ M G = Σ M G eff :             2   lb 8 12 ft = 1 2 20 g 8 12 2 α B

α B = 0.3 g ,

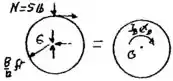
Correia Eq. (4)

P - F A - F B = 0

F A = P - F B

= 3.60 - 2

= 1.60   lb

Nossa análise do disco A, portanto, é válida. Usando a Eq. (2)

Nós temos

1.60   l b = 5 6 α A g

α A = 1.92   g

Resposta

O deslizamento ocorre entre o disco B e a correia.

α B = 9.66   rad/ s 2

Desde  F A < F M , não há deslizamento entre A e a correia.

α A = 61.8   rad/ s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento do volante enquanto rola para cima a cremalheira fixa sobre o seu núcleo dentado é controlado por meio do cabo periférico pela roda motora D , que gira no sentido anti-horário na taxa cons
O movimento vertical da plataforma de trabalho é controlado pelo movimento horizontal do pino A . Se A possui uma velocidade v 0 para a esquerda, determine a velocidade vertical v da plataforma para q
Calcule a velocidade angular ω da barra esbelta A B como uma função da distância x e da velocidade angular constante ω 0 do tambor.
Um quebra-molas está sendo instalado em uma estrada horizontal para lembrar aos motoristas do limite da velocidade existente. Se o motorista do carro sente em G uma aceleração vertical da mesma ordem
Em um mecanismo projetado para converter movimento linear em movimente angular, o cilindro hidráulico fornece ao pino A uma velocidade constante para baixo v durante um curto intervalo de movimento. D