Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 42

Em uma corrida de barcos, o barco A está 36 m a frente do barco B e ambos estão viajando a uma velocidade escalar constante de 168 k m / h . Em t = 0 , os barcos aceleram as taxas constantes, determine (a) a aceleração de A, (b) a aceleração de B.

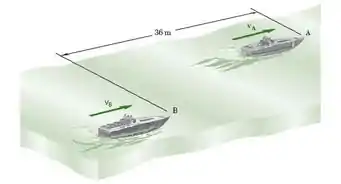
Passo 1

E ai pessoal tudo certinho? O enunciado pede que a gente determine (a) a aceleração de A, (b) a aceleração de B.

Passo 2

  1. Temos: v A = ( v A ) 0 + a A t

    2. ( v A ) 0 = 1 68   k m / h = 46,6667   m / s

    Em: t = 8 s : v A = 60,3504   m / s

    Então

    60,35 s = 46,6 s + a A   x   ( 8 s ) = 1,6764   m / s ²

    Passo 3

  2. Temos: x A = ( x A ) 0 + ( v A ) 0 t + 1 2 a A t ² ( x A ) 0 = 36   m

E x B = 0 + ( v B ) 0 t + 1 2 a B t ² ( v B ) 0 = 46,9392

Em t = 8 s : x A = x B 36 + ( 46,9392 )   x   ( 8 s ) + 1 2   x   ( 1,6764   m / s ² )   x   ( 8 s ) ²

( 46,9392   m / s )   x   ( 8 s ) + 1 2 a B   x   ( 8 s ) ² =   2,8194   m / s ²

Resposta

  1. a A = 1,6764   m / s ²
  2. a B = 2,8194   m / s ²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o helicóptero do Problema 11.169 determinou-se que, quando ele se encontrava no ponto B, a distância e o angulo de rampa desse helicóptero eram r = 900 m e θ = 20°, respectivamente. Quatro segund
O movimento bidimensional de uma partícula e definido pelas relações r = 2a cos θ e θ = bt2/2, onde a e b são constantes. Determine (a) as intensidades da velocidade e a aceleração em qualquer instant
A trajetória de uma partícula P e um elipse definida pelas relações r = 2 /(2 - cos θ ) e θ = π t, onde r e expresso em metros, t em segundos e θ em radianos. Determine a velocidade e a aceleração da
Na posição mostrada na figura, o colar B se movimenta para baixo com uma velocidade de 300 m m / s . Determine (a) a velocidade do colar A, (b) a velocidade da porção C do cabo, (c) a velocidade relat
O elevador mostrado a figura se movimenta para baixo com velocidade constante de 4,5 m / s . Determine (a) a velocidade do cabo C, (b) a velocidade do contra peso W, (c) a velocidade relativa do cabo