Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 139
3/139) A força é aplicada ao sistema , que está inicialmente em repouso . Determine as velocidades de e após ter se deslocado .
Passo 1
Bom pessoal , para resolvermosesse tipo de exercício precisamos primeiramente calcular o comprimento total do cabo do sistema . E para isso , precisamos definir que :
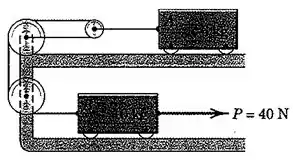
é a distância entre o centro da polia polia maior (mais elevada) e o centro da polia que conecta o carinho de cima .
é a distância entre o centro da polia maior (menos elevada) e o ponto de contato do cabo com o carrinho de baixo .
Com isso definido , temos que o comprimento do cabo é dado por :
Passo 2
Então galera , agora derivamos a equação do comprimento do cabo para obtermos uma relação com as velocidades :
Sabendo-se que e :
Aplicando a lei de trabalho-energia :
Sendo assim ,
Substituindo os valores que já conhecemos :
Logo ,
Resposta
De boa galera? Então bora resolver mais exercícios como esse!