Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 150
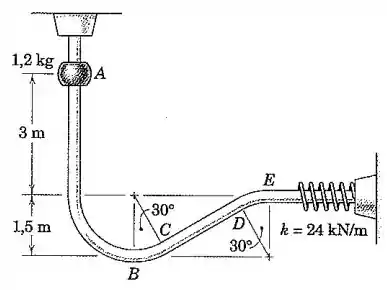
O cursor de do sistema do Prob. 3/149 é liberado a partir do repouso na posição e desliza sem atrito ao longo da guia no plano vertical. Determine a força normal exercida pela guia sobre o cursor
(a) pouco antes que este passe o ponto ,
(b) logo depois que este passa o ponto e
(c) pouco antes que este passe o ponto .
Passo 1
(a) Nesse caso, como não há atrito, a energia mecânica do sistema se conserva. Vamos considerar a altura de como a altura zero do sistema, beleza?
Sabendo a velocidade no ponto , e que um pouco antes desse ponto a trajetória ainda era circular, podemos calcular a aceleração normal nesse ponto ao aplicar a Segunda Lei de Newton:
Passo 2
(b) Um pouco depois do ponto , ainda consideraremos a velocidade , mas agora não há mais aceleração normal à trajetória, é como se a partícula estivesse subindo um plano inclinado de . Então:
Passo 3
(c) Primeiro, vamos calcular a velocidade no ponto , usando a conservação de energia:
Perceba que, um pouco antes do ponto , a trajetória faz parte de uma circunferência (entre os pontos e ). Então o cálculo da normal é parecido com o do item (a), com a diferença de que agora a aceleração normal está dirigida para baixo:
O sinal negativo aqui indica que a normal deve ser para baixo, ao contrário do que supusemos para o nosso cálculo. Então, em módulo a força é:
Resposta
(a)
(b)
(c)