Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 99
Usando os princípios de conservação da energia e da quantidade de movimento angular, resolva o item a do Problema Resolvido 12.8.
Passo 1
Oi, gente! Tudo joinha?
Esse problema deve ser resolvido como base no Problema Resolvido 12.8, porém, utilizando os princípios de conservação da energia e da quantidade de movimento angular. Então, vamos lá!
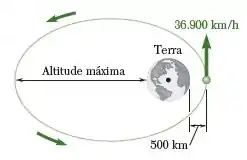
O satélite é lançado paralelamente à superfície da terra e o enunciado fornece os dados:
Sabemos que o raio da Terra é:
Então, calculando o raio de lançamento, temos:
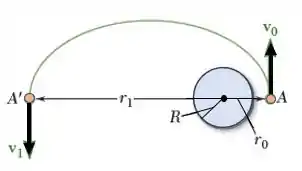
Vamos aplicar agora a conservação do momento angular:
Observe que a posição inicial é no ponto e a posição onde o raio é máximo no ponto .
Passo 2
Calculando a energia cinética e potencial.
Ponto A:
Cuidado para não confundir a massa com a unidade metros! Fique atento!
Aplicando agora a Eq. 13.17, usada para a energia potencial quando a variação da força da gravidade não pode ser desprezada:
No caso de um corpo de massa sujeito à atração gravitacional da Terra, o produto , pode ser expresso de acordo a Eq. (12.29),
em que e são, respectivamente, a massa e o raio da Terra.
Sabemos que,
e
Então, substituindo na Eq. (12.29), temos,
Substituindo em :
Ponto A’:
Passo 3
Em posse das energias cinética e potencial, vamos aplicar o princípio da conservação da energia:
Substituindo pela expressão obtida anteriormente:
Resolvendo a equação do segundo grau, chegamos ao resultado para :
O problema solicita a altitude máxima, portanto:
O resultado do exemplo e esse aqui obtido não deram exatamente iguais devido as aproximações feitas durante os cálculos.