Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 96

Para o movimento descrito no Problema 13.96, determinar (a) a máxima distância entre a origem e o colar, (b) a velocidade correspondente. Dica: Resolva por tentativa e erro a equação obtida para r .)

Passo 1

Oooi, pessoal!

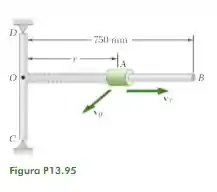
Nesse problema o nosso objetivo é determinar máxima distância entre a origem e o colar A , e a velocidade correspondente. Pelo enunciado, sabemos que temos que encontrar uma equação para r m á x e, por meio de tentativa e erro, chegar ao resultado. Primeiro vamos anotar os dados que são fornecidos.

m = 5   k g

k = 800   N / m  

r i n d e f o r m a d o = 450   m m = 0,45   m

r 1 = 300   m m = 0,3   m

v θ 1 = 5   m / s

v r 1 = 0

Sabendo de tais dados, agora vamos calcular a deflexão da mola na posição inicial do colar (Posição 1). O problema nos diz que ele é posto em movimento com r 1 = 0.3   m e r i n d e f o r m a d o = 0.45   m . Observe que ele parte de uma posição na qual a mola está comprimida.

x 1 = r 1 - r i n d e f o r m a d o

x 1 = 0,3 - 0,45 = - 0,15   m

Sendo v r 1 = 0 , então

v 1 = v θ 1 = 5   m / s

Calculando a energia cinética nesse ponto:

T 1 = 1 2 m v 1 2

T 1 = 5 ⋅ 5 2 2 = 6 2 , 5   J

E a energia potencial:

V 1 = 1 2 k x 1 2

V 1 = 800 ⋅ ( - 0.15 ) 2 2 = 9   J

Passo 2

Vamos chamar de Posição 2 o ponto máximo até onde o colar A pode chegar partindo da origem.

r m á x = r 2

Calculando a deflexão, temos

x 2 = r 2 - r i n d e f o r m a d o

x 2 = r 2 - 0,45

No ponto máximo, a componente radial da velocidade é zero, dessa forma, concluímos que

v 2 = v θ 2

Vamos agora calcular a energia cinética T 2 e a energia potencial V 2 .

T 2 = 1 2 m v 2 2

T 2 = 5 v θ 2 2 2 = 2,5 v θ 2 2

V 2 = 1 2 k x 2 2

V 2 = 800 r 2 - 0,45 2 2 = 400 r 2 - 0,45 2

Passo 3

O próximo passo é aplicar o princípio da conservação do momento angular. Isolando v θ 2 vamos encontrar uma expressão que, posteriormente, substituiremos na expressão que obtivemos para T 2 .

r 1 m v θ 1 = r 2 m v θ 2

Lembre-se que v θ 2 = v 2 ,

v 2 = r 1 v θ 1 r 2 = 0,3 ⋅ 5 r 2

v 2 = 1,5 r 2

Passo 4

Em posse das energias cinéticas e potenciais, vamos aplicar agora o princípio da conservação da energia.

T 1 + V 1 = T 2 + V 2

6 2 , 5 + 9 = 2,5 v θ 2 2 + 400 r 2 - 0,45 2

7 1 , 5 = 2,5 ⋅ 1,5 r 2 2 + 400 r 2 - 0,45 2

7 1 , 5 = 5,625 r 2 2 + 400 r 2 - 0,45 2

Chegamos então à equação

5,625 r 2 2 + 400 r 2 - 0,45 2 - 7 1 , 5 = 0

Passo 5

O problema pede que a equação encontrada seja resolvida por tentativa e erro. Para ter uma base sobre por qual valor começar, observe que no problema anterior encontramos a velocidade para r = 0,52   m , então vamos iniciar, por exemplo, por r 2 = 0,6   m . Temos que,

f r 2 = 5,625 r 2 2 + 400 r 2 - 0,45 2 - 71,5

Vamos encontrar um valor para r 2 tal que f r 2 = 0 .

Para r 2 = 0,6   m :

f 0,6 = 5,625 0,6 2 + 400 0,6 - 0,45 2 - 71,5 = - 46,875

Para r 2 = 0,7   m :

f 0,7 = 5,625 0,7 2 + 400 0,7 - 0,45 2 - 71,5 = - 35,02

Para r 2 = 0,8   m :

f 0,8 = 5,625 0,8 2 + 400 0,8 - 0,45 2 - 71,5 = - 13,71

Para r 2 = 0,9   m :

f 0,9 = 5,625 0,9 2 + 400 0,9 - 0,45 2 - 71,5 = 16,444

Observe que passamos de zero, então vamos tentar r 2 = 0,85   m :

f 0,85 = 5,625 0,9 2 + 400 0,9 - 0,45 2 - 71,5 = 0,285

Esse valor está bem próximo de zero, então, para f x = 0 , o nosso r 2 é aproximadamente

r 2 = 0,849   m = r m á x

Que é a máxima distância entre a origem e o colar A .

Passo 6

Em posse de r m á x , sabendo que

v 2 = 1,5 r m á x

Encontramos a velocidade máxima correspondente

v m á x = 1,5 0,849 = 1,766   m / s

Resposta

a )   r m á x = 0,849   m

b )   v m á x = 1,766   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra fina AB de 12,5 kg está fixada à mola BC, que tem um comprimento não deformado de 1,2 m. Se a barra é liberada do repouso quando θ = 30°, determine sua velocidade angular no instante em que a
Quando a barra fina AB de 10 kg está horizontal, ela está em repouso e a mola não está deformada. Determine a rigidez k da mola, de modo que o movimento da barra seja parado momentaneamente após ela h
A montagem consiste de duas barras de 4 kg que estão conectadas por pinos aos dois discos de 5 kg. Se as barras são liberadas do repouso quando θ = 60°, determine suas velocidades angulares no instant
A transmissão por fluido de um caminhão de 15000 kg permite que o motor forneça potencia constante para as rodas traseiras. Determine a distancia necessária para o caminhão, rodando em uma estrada pla
O carrinho de mina de 1,2 Mg está sendo puxado pelo guincho M montado no carrinho. Se o guincho gera uma potencia de saida constante de 30Kw. Determine a velocidade do carrinho no instante em que ele