Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 92
Observações mostram que um corpo celeste que viaja a parece estar descrevendo um círculo em torno do ponto de raio igual a anos-luz. Suspeita-se que o ponto seja uma concentração de massa muito densa conhecida como buraco negro. Determine a razão entre a massa de e a massa do Sol. (A massa do Sol é vezes a massa da Terra e um ano-luz é a distância percorrida pela luz em um ano à velocidade de .)
Passo 1
Oi, pessoal! Vamos para a resolução de mais um problema?
Primeiro vamos fazer um esboço da situação enunciada no problema.
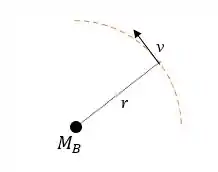
Em que é a massa do ponto , é o raio do círculo que o corpo celeste descreve em torno de e é a velocidade na qual ele viaja. O problema pede que determinemos a razão entre a massa de e a massa do Sol, .
Nos são fornecidos os seguintes dados:
Um ano luz é a distância percorrida pela luz em um ano à velocidade de . Portanto, sendo 60 anos luz, temos:
Passo 2
A força centrípeta que o Sol exerce sobre um planeta de massa , que se move com velocidade à uma distância do Sol, é dada por:
A partir disso, Newton deduziu que, dois corpos com centros a uma distância um do outro se atraem com força proporcional às suas massas e inversamente proporcional ao quadrado de (Lei de Newton da Gravitação Universal), conforme mostra a Eq. (12.27),
Dessa forma,
Passo 3
No caso de um corpo de massa sujeito à atração gravitacional da Terra, o produto , pode ser expresso de acordo a Eq. (12.29),
em que e são, respectivamente, a massa e o raio da Terra.
Sabemos que,
e
Então, substituindo na Eq. (12.29), temos,
O enunciado nos informa que a massa do Sol é 330000 vezes a massa da Terra, então,
e, portanto,
Passo 4
Substituindo na equação
encontramos a relação solicitada no problema: