Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 17
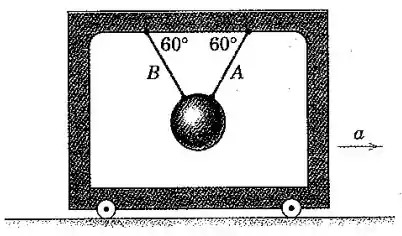
A esfera de aço está suspensa na estrada acelerada pelas duas cordas e . Determine a aceleração da estrutura que fará com que a tração em seja o dobro daquela em .
Passo 1
Galera, as forças na vertical estão em equilíbrio, ou seja:
Mas, pelo enunciado, temos , então:
Passo 2
Aplicando a Segunda Lei de Newton na direção horizontal, temos
Porém, já sabemos que :
Podemos jogar aqui a expressão de obtida no passo anterior:
Resposta
Exercícios de Livros Relacionados
Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo θ e a bola em questão, a aceleração da bola ao longo da inclinação é constante em 0,25 g , dirigi
Uma força de desaceleração atua sobre uma partícula que inicialmente se desloca com uma velocidade de 100m / s e fornece uma desaceleração como a registrada pela leitura do osciloscópio mostrado na fi
Uma partícula viajando em uma linha reta encontra uma força que a retarda e provoca a redução de sua velocidade segundo v = 20 e - t / 10m / s , onde t é o tempo em segundos durante o qual a força age
Uma motocicleta parte do repouso com uma aceleração inicial de 3 m / s 2 e a aceleração então varia com a distância s como mostrado na figura. Determine a velocidade v da motocicleta quando s = 200m .
Uma partícula oscila ao longo de uma linha reta com uma velocidade variando senoidalmente em milímetros por segundo dada por v = 16 sen π t / 6 , onde t é em segundos. Se o deslocamento da partícula