Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 184

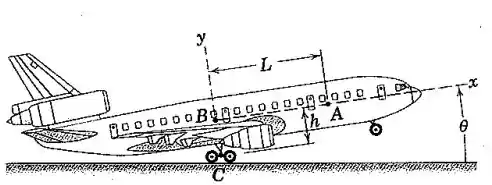
Próximo do final de sua corrida para decolagem, o avião está girando (arfagem do nariz para cima) imediatamente antes de levantar voo. A velocidade e a aceleração da aeronave, expressas em termos do movimento do conjunto das rodas C, são v C   e   a C , ambos dirigidos horizontalmente para frente, O ângulo de arfagem é θ , e a taxa de arfagem ω = θ ˙ está aumentando na taxa α = θ ¨ .   Se uma pessoa A está caminhando para frente no corredor central com velocidade L ˙ e aceleração L ¨ , ambos medidos em frente em relação à cabine, desenvolva expressões para a velocidade e aceleração de A conforme vistas por um observador fixo no solo.

Passo 1

Bom pessoal, primeiro vamos parametrizar as variáveis de acordo com o enunciado:

r = L i ^

r ˙ = v r e l = L ˙ i ^

r ¨ = a r e l = L ¨ i ^

ω = θ ˙ k ^

α = θ ¨ k ^

A velocidade e aceleração das rodas C:

v C = v C ( c o s θ   i ^ - s e n θ   j ^ )

a C = a C ( c o s θ   i ^ - s e n θ   j ^ )

Agora, vamos usar a equação da velocidade relativa entre os pontos A e C:

v A = v C + ω × r A C + v r e l

v A = v C c o s θ   i ^ - s e n θ   j ^ + ω k ^ × L i ^ + h j ^ + L ˙ i ^

Rearrumando a equação:

v A = v C c o s θ - ω h + l ˙ i ^ + - v C s e n θ + ω L j ^   m / s

Passo 2

Agora, vamos para o cálculo das acelerações.

Vamos usar a equação da aceleração relativa entre os pontos A e C:

a A = a C + α × r A C + ω × ω × r A C + 2 ω × v r e l + a r e l

Substituindo os valores, temos que:

a A = a C c o s θ   i ^ - s e n θ   j ^ + α k ^ × L i ^ + h j ^ - ω 2 L i ^ + h j ^ + 2 ω k ^ × L ˙ i ^ + L ¨ i ^

a A = a C c o s θ - α h - L ω 2 + L ¨ i ^ + a C s e n θ + α L - h ω 2 + 2 L ˙ ω j ^   m / s 2

Resposta

v A = v C c o s θ - ω h + l ˙ i ^ + - v C s e n θ + ω L j ^   m / s

a A = a C c o s θ - α h - L ω 2 + L ¨ i ^ + a C s e n θ + α L - h ω 2 + 2 L ˙ ω j ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o cursor e a manivela do Prob. 5/209 desenvolva a expressão para a aceleração a A do pistão (admitida positiva para a direita) como uma função de θ para ω = θ ˙ = c o n s t a n t e . Substitua os
Um torque constante M ultrapassa o momento em torno de O devido à força F sobre o embolo, e resulta em uma aceleração angular θ ¨ = 100 1 - c o s θ r a d / s 2 . Se a manivela AO é liberada a partir d
A manivela gira no sentido horário na taxa constante θ ˙ = 3r a d / s . A haste AB passa através do cursor articulado em C. Determine a velocidade máxima v em que AB passa através do cursor e o valor
Para a configuração de cursor e manivela apresentada, desenvolva a expressão para a velocidade v A do pistão (admitida positiva para a direita) como função de θ . Substitua os dados numéricos do Exemp
A barra AO gira em torno do ponto fixo O com velocidade constante de 0,8 rad/s. O pino A é fixo na barra AO e está encaixado na ranhura do membro BD, que gira em torno de um eixo através do ponto B. D