Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 181

Uma câmara de teste A é utilizada para estudar enjoo. A câmara é capaz de oscilar em torno de um eixo horizontal através de O de acordo com θ = θ 0 s e n 2 π f 1 t , e, ao mesmo tempo, possui um movimento linear   y = y 0 s e n 2 π f 2 t em relação à estrutura. Para um determinado conjunto de testes, as amplitudes estão reguladas em θ 0 = π 4 e y 0 = 150   m m , enquanto as frequências correspondentes são f 1 = 1 4   c i c l o s / s e f 2 = 1 2 c i c l o s / s . Determine a expressão vetorial para a aceleração do ponto C na câmara no instante em que t = 2s.

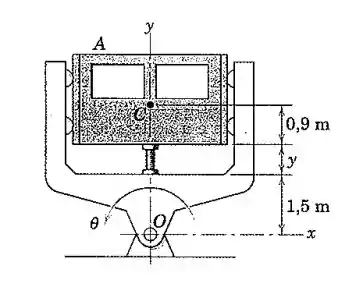
Passo 1

Bom pessoal, esta questão pode assustar de início por apresentar movimentos harmônicos, que usa senos e frequência. Por isso é importante escrever os dados e ir juntando as peças.

Vamos começar colocando as condições iniciais e os valores das frequências nas equações de movimento.

θ = θ 0 s e n 2 π f 1 t       ;       θ 0 = π 4     ;           f 1 = 1 4

θ = π 4 s e n π 2 t  

y = y 0 s e n 2 π f 2 t         ;       y 0 = 0,15       ;       f 2 = 1 2

y = 0,15 s e n π t

Agora, vamos calcular a velocidade angular e a aceleração angular através das derivadas em função do tempo de θ :

θ ˙ = ω = π 2 8 c o s π 2 t

θ ¨ = α = - π 3 16 s e n π 2 t  

Da mesma forma, vamos calcular a v r e l   e   a   a r e l a partir das derivadas de y :

y ˙ = v r e l = 0,15 π   c o s π t

y ¨ = a r e l = - 0,15 π 2   s e n π t

Passo 2

Neste passo, vamos para o cálculo das acelerações. Mas antes, vamos escrever os vetores no instante t = 2s:

r = 1,5 + y + 0,9 = 2,4 + 0,15 s e n 0 = 2,4 j ^   m

θ = π 4 s e n π = 0

θ ˙ = ω = π 2 8 c o s π = - π 2 8   k ^   r a d / s

θ ¨ = α = - π 3 16 s e n π = 0

y ˙ = v r e l = 0,15 π   c o s 2 π = 0,15 π j ^   m / s

y ¨ = a r e l = - 0,15 π 2   s e n 2 π = 0

Agora, vamos usar a equação da aceleração relativa entre C e O:

a C = a O + α × r + ω × ω × r + 2 ω × v r e l + a r e l

Substituindo os valores:

a C = 0 + 0 - - π 2 8 2 2,4 j ^ + 2 - π 2 8 k ^ × 0,15 π j ^ + 0

a C = - 0,3 π 3 8 j ^ + 0,3 π 3 8 i ^   m / s 2

a C = 0,3 π 3 8 i ^ - π   j ^   m / s 2

Resposta

a C = 0,3 π 3 8 i ^ - π   j ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando a barra A B está na posição mostrada, o anel A se desloca com uma velocidade v A = 5 im / s e aceleração a A = 1 im / s 2 . Determine a aceleração do anel B nesse instante. Suponha que a veloci
No instante θ = 30 ° , a estrutura do guindaste e a lança A B giram com uma velocidade angular constante ω 1 = 1,5r a d / s e ω 2 = 0,5r a d / s , respectivamente. Determine a velocidade e a aceleraçã
No instante mostrado, a base do braço robótico gira em torno do eixo z com uma velocidade angular ω 1 = 4 r a d / s , a qual está aumentando a ω ˙ 1 = 3r a d / s 2 . Além disso, a lança B C gira com u
Se a manivela B C gira com uma velocidade angular ω B C = 6r a d / s , determine a velocidade do anel em A . Suponha que a velocidade angular de A B é perpendicular à barra.
A barra A B está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A se desloca para cima com uma aceleração a A = 2 km / s 2 , determine a aceleração angular da barra A B e a int