Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 174 (b)
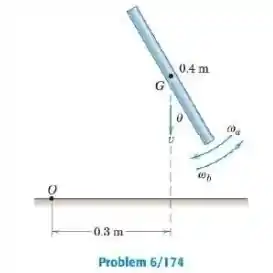
O centro de massa da barra esbelta de massa e comprimento está caindo verticalmente com uma velocidade no instante representado. Calcule a quantidade de movimento angular da barra em relação ao ponto se a velocidade angular da barra é (b) no sentido anti-horário.
Passo 1
A quantidade de movimento angular em relação ao centro de massa é dada por
A quantidade de movimento linear, por sua vez, é dada por
Passo 2
A quantidade de movimento angular em relação a um ponto qualquer é dada por
Substituindo valores, obtemos
Resposta
Exercícios de Livros Relacionados
Uma esfera de raio r e massa m é colocada sobre um piso horizontal sem velocidade linear, mas com velocidade angular ω 0 no sentido horário. Representando por μ k o coeficiente de atrito cinético entr
Uma esfera de raio r e massa m é lançada ao longo de uma superfície horizontal rugosa com as velocidades iniciais mostradas na figura. Para que a velocidade final da esfera seja nula, expresse (a) a i
Um disco de 1,25 kg e 100 mm de raio está preso ao suporte BCD por meio de pequenos eixos montados em mancais em B e D. O suporte de 0,75 kg tem raio de giração de 75 mm em relação ao eixo x. Inicialm
Admitindo que o rotor de cauda do Problema 17.84 esteja operando e que a velocidade angular da cabine permaneça nula, determine a velocidade horizontal final da cabine quando a velocidade das pás prin
Dois painéis A e B são ligados por dobradiças a uma placa retangular e mantidos por um fio como mostra na figura. A placa e os painéis são feitos do mesmo material e têm a mesma espessura. Sabendo que