Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 137
Os cursores A e B são conectados por um fio de comprimento de 525 mm e podem deslizar livremente, sem atrito, sobre as hastes. Se a força é aplicada ao colar A, determine a tensão no fio quando , a intensidade da força requerida para manter o equilíbrio do sistema.
Passo 1
Vamos começar o exercício desenhando o DCL para os cursores A e B:
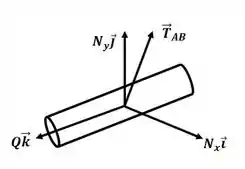
Aplicando o somatório de forças para o cursor A:
E o somatório de forças para o cursor B:
Agora precisamos escrever o vetor tensão em termos de suas coordenadas, para isso, precisamos primeiro escrever o vetor que liga esses pontos, então:
Calculando o módulo desse vetor:
Sendo assim, podemos escrever o vetor tensão como:
Passo 2
Substituindo o valor da tensão na equação de equilíbrio de forças do passo 1 para cursor A, temos:
Agora vamos separar as componentes e :
Substituindo o valor de P dado no enunciado, temos:
Da mesma forma, para o cursor B:
Separando as componentes e :
Passo 3
Finalmente, da segunda equação para o cursor A, temos:
E, substituindo esse valor na última equação para o cursor B: