Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 17
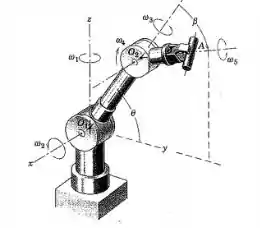
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x com a velocidade angular . O braço de controle O2A gira em torno do eixo O1-O2 com velocidade angular . Finalmente, as garras giram em torno do eixo O2-A com velocidade angular w5. Os módulos de todas as velocidades angulares são constantes. Para a configuração mostrada, determine o módulo w da velocidade angular total para quando , se , e w3=w4=w5=0. Expresse também a aceleração angular do braço O1O2 como um vetor.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que esse robô doidão tem o eixo rodando a uma velocidade constante e que o eixo também está rodando, e nos pedeo módulo da velocidade angular e a aceleração angular. Viu?? Parece que é muita coisa, mas nem é tão difícil assim. Bora lá fazer?? Partiu??
Passo 2
Nosso primeiro passo será determinar a nossa velocidade angular total. Como ele nos diz que 3 das 5 velocidades são iguais a zero, só temos então w1 e w2 para nos preocuparmos, certo?? Então, teremos que a velocidade angular total será a soma dessas duas.
Agora, só tirar o módulo daí!!
Passo 3
Pronto!! Com isso, podemos achar qual a nossa aceleração angular.