Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 1

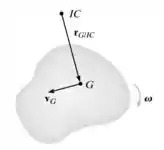
Em um dado instante, o corpo de massa m com uma velocidade angular ω e uma velocidade de seu centro de massa vg. Demonstrar que sua energia cinética total se dá por T = 1 2 . I i c . ω ² , onde Iic é o seu momento de inércia calculado em relação a seu eixo instantâneo de velocidade nula a uma distância rG/Ic de seu centro de massa.

Passo 1

Temos, por definição que:

T = 1 2 × m × v × g 2 + 1 2 × I g × ω 2

Porém, sabe-se que a velocidade se seu centro de massa, se dá pela multiplicação de sua velocidade angular pela distância de seu centro de massa ao seu eixo instantâneo de velocidade nula, dado por rG/Ic, logo teremos que:

v g = ω × r G / I c

Com isso, teremos uma nova equação, onde:

T = 1 2 × m × ( ω × r G / I c ) ² + 1 2 × I g × ω 2                   ( 1 )

Passo 2

Rearranjando a equação 1, temos:

T = 1 2 ( m × ( ω × r G / I c ) ² + I g × ω 2 )

Organizando mais ainda, temos:

T = 1 2 × ω ² ( m × ( r G / I c ) ² + I g )                 ( 2 )

Sabendo que o momento de inércia do corpo se dá como, por definição:

I i c =   m × ( r G / I c ) ² + I g                 ( 3 )

Então podemos substituir (3) em (2):

T = 1 2 × ω 2 × I i c

Resposta

A enercia cinética do corpo será dada por T = 1 2 × ω 2 × I i c , onde ω é sua velocidade angular e Iic é seu momento de inercia com relação ao seu eixo instantâneo de velocidade nula.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tambor tem massa de 50k g e raio de giração em relação ao pino em O , k O = 0,23m . Partindo do repouso, o bloco suspenso B , de 15k g , é deixado cair por 3m , sem que se aplique o freio A C D . De
O disco semicircular uniforme de 15 kg é sustentado, na posição de equilíbrio mostrada, pelos dois cabos que estão enrolados em volta de seus cubos anexos e são guiados até as molas idênticas. Cada mo
O disco circular uniforme de 45 kg com sua barra esbelta de 9 kg presa é liberado a partir do repouso na posição mostrada e rola sem deslizar sobre a superfície horizontal. Calcule a velocidade v o qu
O mecanismo mostrado se move no plano vertical. A barra vertical AB tem uma massa de 4,5 kg, e cada uma das duas hastes tem uma massa de 2,7kg com centro de massa em G e com um raio de giração de 250
O mecanismo é constituído por duas barras esbeltas e se move no plano horizontal sob influência da força P . A barra O C tem uma massa m e a barra A C tem massa 2 m . O bloco deslizante em B tem massa