Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 147
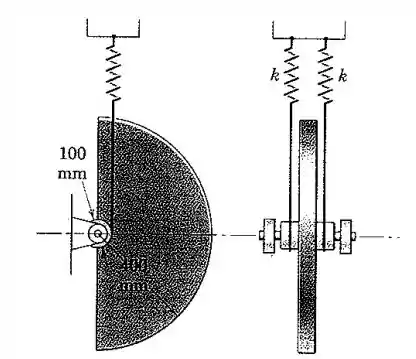
O disco semicircular uniforme de 15 kg é sustentado, na posição de equilíbrio mostrada, pelos dois cabos que estão enrolados em volta de seus cubos anexos e são guiados até as molas idênticas. Cada mola possui uma rigidez . Se o disco é girado em de modo que o seu centro de massa fique na posição mais baixa possível e em seguida é liberado a partir do repouso, calcule a velocidade angular do disco quando passa pela posição de equilíbrio. Despreze a massa dos cubos e do eixo.
Passo 1
Pessoal, primeiramente, vamos analisar as forças na posição de equilíbrio, que é a mostrada na figura.
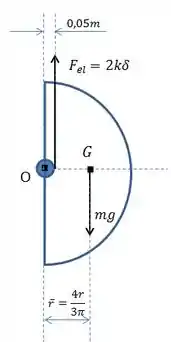
É importante nesse exercício saber a posição do centro de massa de semicírculos.
Para encontrar o valor da força elástica atuando no sistema, vamos fazer o somatório de momentos em relação a O:
Como são duas molas em paralelo, temos que a constante equivalente da mola é a soma das duas (2k). Podemos então descobrir a deflexão inicial das molas:
Passo 2
Agora vamos representar o sistema nas posições dadas no enunciado:
- Primeiro, o centro de massa do disco está o mais baixo possível. Bom, isso vai ocorrer quando o disco estiver na horizontal.
- Após, o enunciado pede para calcular a velocidade angular quando o disco passa pela posição de equilíbrio, que é a mostrada acima.
Veja a figura:
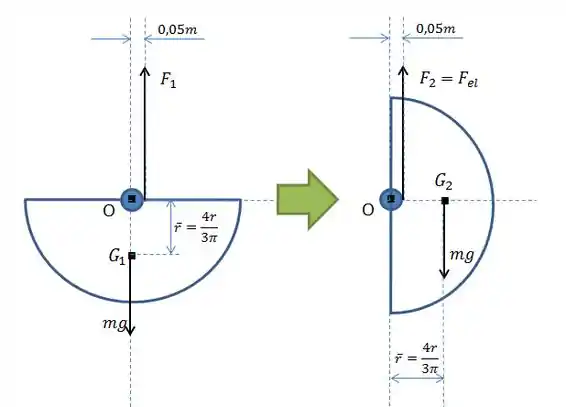
Bom, agora vamos elaborar as equações de energia para as duas situações:
Posição 1:
A energia cinética nesta posição é nula, pois não há velocidade atuando no disco.
A energia potencial será considerada zero nesta condição, justamente por está no ponto mais baixo. Agora vamos para a energia potencial elástica. Para o disco ser colocado nessa posição, a polia O teve que ser girada , portanto as molas tiveram uma deflexão adicional de ¼ do perímetro da polia.
Fazendo o somatório de energia para o caso 1:
Posição 2:
A energia cinética nesta posição será apenas rotacional, já que não há translação do disco.
A energia potencial gravitacional e a energia potencial elástica serão de acordo com suas altura e deflexão estática, respectivamente.
Por conservação de energia, podemos igualar o instante 1 ao instante 2: