Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 153

O disco circular uniforme de 45 kg com sua barra esbelta de 9 kg presa é liberado a partir do repouso na posição mostrada e rola sem deslizar sobre a superfície horizontal. Calcule a velocidade v o quando o centro de massa da barra está diretamente abaixo do centro O do disco.

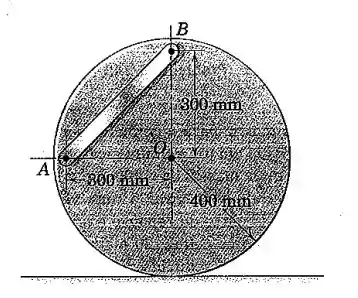
Passo 1

Pessoal, neste exercício temos que analisar as duas situações do enunciado. Vamos começar com o sistema na posição mostrada na figura.

Instante 1

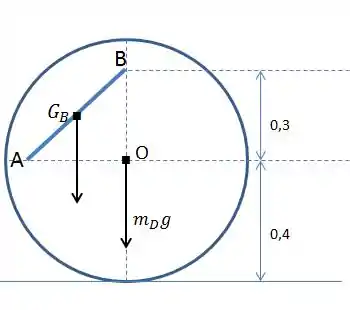
Como o sistema parte do repouso, a energia cinética vale zero neste instante.

Já a energia potencial gravitacional será a soma das energias de cada elemento (a barra e o disco). Entretanto, vamos “ignorar” a energia gravitacional do disco, pois no instante 1 e no 2 sua altura é a mesma, então sua energia gravitacional não irá variar. Vamos então calcular a energia neste instante:

E 1 = m D g h = 9 9,81 0,4 + 0,3 2 = 48,56   J

Passo 2

Agora vamos para o instante 2. Veja como o sistema está nessa posição.

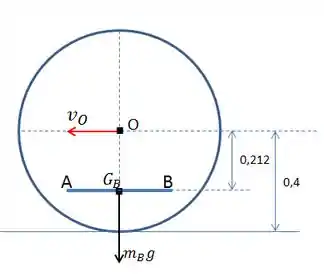
Neste instante, tanto a barra quanto o disco estão transladando e rotacionando. Portanto, terão duas componentes para a energia cinética: a de rotação e a de rotação.

T = T D + T B

T = 1 2 m D v O 2 + 1 2 I O ω 2 + 1 2 m B v B 2 + 1 2 I B ω 2

Agora precisamos encontrar relações para as velocidades absolutas e para a angular.

Como não há deslizamento, então o ponto de contato do disco com o chão é o centro instantâneo de velocidade nula. Desta forma, podemos tirar a relação para a velocidade angular do sistema:

ω = v O r = v O 0,4 = 2,5 v O

Da mesma forma, podemos calcular a velocidade absoluta da barra:

v G = ω × r G C

v G = 0,4 - 0,212 0,4 v O = 0,47 v O

Além disso, também é importante conhecer os momentos de inercia:

I O = 1 2 m D r 2 = 1 2 45 0,4 2 = 3,6   k g m 2

I B = 1 12 m B l 2 = 1 12 9 0,3 2 2 = 0 , 135   k g m 2

Agora sim podemos substituir na equação da energia cinética:

T = 1 2 45 v O 2 + 1 2 3,6 ( 2,5 v O 2 ) 2 + 1 2 9 0,47 v O 2 + 1 2 0 , 135 ( 2 , 5 v O 2 ) 2

T = v O 2 22,5 + 11,25 + 0,994 + 0,422 = 35,16 v O 2

Já a energia potencial gravitacional da barra fica:

V = m B g h 2 = 9 9,81 0,4 - 0,212 = 16 , 60

Logo a energia no instante 2 vale:

E 2 = 16,60 + 35,16 v O 2

Por conservação de energia, podemos igualar o instante 1 ao instante 2:

E 1 = E 2

48,56 = 16,60 + 35,16 v O 2

v O = 0,954   m / s

Resposta

v O = 0,954   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A alavanca O A de 5,5k g com 250m m de raio de giração em relação a O está inicialmente em repouso na posição vertical ( θ = 90 ° ), onde a mola anexa de rigidez k = 525N / m está sem deformação. Calc
O disco B rola sem deslizar para baixo na inclinação A , que se desloca com velocidade v . Descreva o trabalho realizado pelas forças normal e de atrito que atuam sobre o disco para os casos (a) v = 0
O disco semicircular de massa m = 2k g está montado no aro leve de raio r = 150m m e é liberado a partir do repouso na posição (a). Determine a velocidade angular ω do aro e a força normal N sob o aro
O tambor de 375m m de raio e seu eixo possuem uma massa de 41k g e um raio de giração de 300m m em relação ao eixo de rotação. Um total de 18m de cabo de aço flexível com uma massa de 3,08k g por metr
A roda é constituída por um aro de 4k g com 250m m de raio, com cubo e raios de massa desprezível. A roda está montada no garfo O A de 3k g com centro de massa em G e com um raio de giração em relação