Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 4

O carretel de cabo que está em repouso, tem massa de 200Kg e um raio de giração Kg=325mm, quando uma força P=400N é aplicada no cabo conforme mostra a figura. Considerando que ele está sobre dois oequenos rolos, determinar sua velocidade angular quando 8m de cabo são puxados. Desconsiderar o atrito e a massa dos rolos e do cabo desenrolado.

Passo 1

Analisando as reações ocorrendo no sistema, temos:

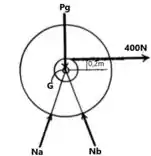
Desconsiderando a massa do rolos, teremos que o somatório das energias presentes no sistema quando este está em repouso, será igual apenas à energia cinética do carretel Tg.

T t o t a l 1 + ∑ U 1 - 2 = T t o t a l 2

Assim, sabendo que no estágio 1 o sistema está em repouso, temos:

0 + ∑ U 1 - 2 = T g

Logo,

∑ U 1 - 2 = T g

Passo 2

Sabendo que ∑U1-2 será dado pela multiplicação da força com o comprimento desenrolado de cabo, e sabendo que:

T g = 1 2 m g × k G ² × ω ²

Logo teremos que:

400 × 8 = 1 2 × m g × k G ² × ω ²

Como temos kg=325mm e mg=200Kg, teremos:

400 × 8 = 1 2 × 200 × 0,325 ² × ω ²

Isolando ω, temos:

ω = 400 × 8 × 2 200 × 0,325 ² = 17,5 r a d / s

Resposta

A velocidade angular do carretel será de 17,4rad/s, após 8 metros de cabo serem puxados com a força de 400N.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A escada de 15 kg está colocada contra a parede em um ângulo de θ = 45 ° , como mostrado. Se ela é liberada do repouso, determine sua velocidade angular no instante imediatamente anterior a θ = 0 ° .
Determine a velocidade angular das duas barras de 10 kg quando θ = 9 0 ° , se elas são liberadas do repouso na posição θ = 60 ° . Despreze o atrito.
O bloco de 50 kg é transportado por uma distância curta, usando-se dois rolos cilíndricos, cada um com massa de 17,5 kg. Se uma força horizontal P = 125 N é aplicada ao bloco, determine a velocidade d
Quando uma força P = 150 N é aplicada à alavanca do freio, o cilindro A, de 25 kg, está descendo a uma velocidade de 6 m/s. Determine o número de revoluções que a roda B rotacionará antes que seja par
A montagem consiste de duas barras finas de 7,5 kg e de um disco de 10 kg. Se a mola não está deformada quando θ = 45 ° e a montagem é liberada do repouso nessa posição, determine a velocidade angular