Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 20
Dois blocos e têm peso de e , respectivamente. Eles estão apoiados no planos inclinado para qual os coeficientes de atrito estático são e . Determine o ângulo que causará o movimento de um dos blocos. Qual é a força de atrito sob cada um dos blocos quando isso ocorre? A mola tem um rigidez e originalmente não esticada.
Passo 1
O problema pede que encontremos o ângulo máximo antes do movimento e a força atrito em cada um dos blocos.
Beleza, vamos começar fazendo um diagrama de corpo livre em , e vamos decompor a força Peso, assim:
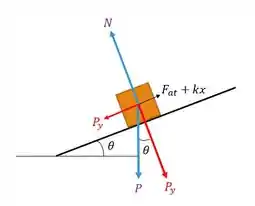
Primeiro a gente pega as forças perpendiculares ao plano inclinado:
Bom, você já deve saber, mas o atrito age em relação a normal, então a gente multiplica a normal com o coeficiente de atrito:
E a gente está estudando um corpo em equilíbrio, né?
Pois, a gente percebe que tem que ser igual ao atrito somado com a força da mola, aí você pensa que complica mas presta atenção nisso:
A MOLA NÃO ESTÁ ESTICADA!!! Uma mola só causa força se estiver esticada.
Então a gente vai conseguir descobri a variável que falta o :
Pegando a inversa trigonométrica na calculador:
Então o ângulo máximo para não então em movimento é .
Assim a gente só substitui no atrito que a gente já tinha encontrado:
Bom, esse é o atrito máximo no bloco.
Passo 2
Então, agora partiu bloco :
Mas agora que a gente já sabe a força da mola e o ângulo nem deve precisar mais que eu ajude, mas vou mesmo assim:
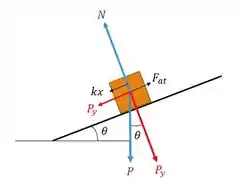
A gente faz do mesmo jeito:
Então a gente já calcula logo o atrito máxima em :
Vamos ver se a resultante do peso paralela a inclinação é menor que o atrito máximo, se for então tá tudo certo e essa resultante é que é a força de atrito atuante, porque esse que a gente encontrou é o máximo antes do corpo entrar em movimento.
Passo 3
Agora, concluindo o ângulo máximo é de , e o bloco fica na iminencia de movimendo, então a força de atrito máxima é igual a resultante do peso que não é compensado pela normal. Assim:
E como em a resultante do peso paralela à inclinação é menor que o atrito máximo, então essa resultante será a força de atrito atuante: