Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 145
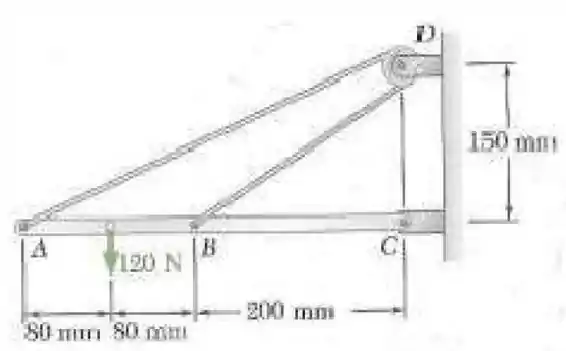
Desprezando o atrito e o raio da polia, determine ( a) a tração no cabo ADB, (b) a reação em C.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Precisamos determinar a tração no cabo ADB e a reção em C.. Para a reação em C encontraremos as componentes .
Olhando para a imagem do enunciado, podemos notar que todas as forças estão em (Newtons) e todas as medidas em mm (milímetros). Portanto não precisaremos fazer conversçoes.
Passo 2
Considere o seguinte diagrama de corpo livre
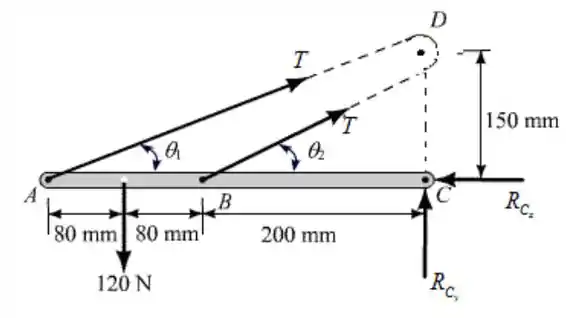
Primeiramente consideraremos os triângulos ACD BCD, para determinar os ângulos
Passo 3
Podemos aplicar o somatório dos momentos em torno de C para determinar a tração T
=0
T indica a tração no cabo e o sinal positivo indica que a direção é a representada no diagrama de corpo livre
Passo 4
Aplicaremos agora o somatório das forças na horizontal para determinar a componente horizontal da reação :
]
indica a reação horizontal no ponto X. Observe que o sinal foi positivo, o que indica que a direção da resultante é a mesma do diagrama de corpo livre, da direita para a esquerda.
Faremos agora o somatório de forças em verticais, temos que:
indica a componente vertical da reação , o sinal negativo indica que o sentido é contrário ao indicado no diagrama de corpo livre, ou seja, de cima pra baixo.
Agora poderemos calcular a reação :
Resposta
- Tração no cabo
- Reação em C