Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 75

Elétrons são emitidos em A com uma velocidade u no ângulo θ para o espaço entre duas placas carregadas. O campo elétrico entre as placas é na direção E e repele os elétrons que se aproximam da placa superior. O campo produz uma aceleração nos elétrons na direção de E de e E / m , onde e é a carga do elétron e m é a sua massa. Determine a intensidade do campo E que permitirá aos elétrons cruzarem metade da abertura entre as placas. Encontre também a distância s .

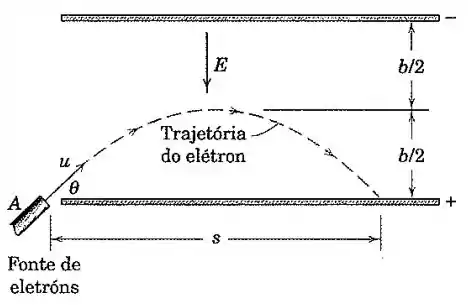
Passo 1

Pessoal, como temos um movimento de aceleração constante na vertical, com a = - e E / m , podemos usar a fórmula:

v 2 - v 0 2 = 2 a d

Adaptando para esse movimento, temos:

v y 2 - u   s e n   θ 2 = 2 - e E m y

v y 2 - u 2 s e n 2   θ = - 2 e E m y

Passo 2

Queremos que o elétron chegue à altura y = b / 2 . A intensidade mínima do campo E que permitirá isso ocorre quando y = b / 2 é a altura máxima do elétron, ou seja, aí teremos v y = 0 .

Bora substituir isso na equação?

0 2 - u 2 s e n 2   θ = - 2 e E m b 2

E = m u 2 s e n 2 θ e b

Passo 3

Show! Por último, podemos encontrar o alcance s usando a fórmula:

s = v 0 2   s e n 2 θ a

onde a = e E / m deve ser a aceleração e v 0 = u . Então:

s = m u 2 s e n 2 θ e E

Substituindo E conforme encontramos no passo anterior, teremos:

s = m u 2 s e n 2 θ e m u 2 s e n 2 θ e b = b   s e n ( 2 θ ) s e n 2 θ = b ( 2   s e n   θ cos ⁡ θ ) s e n 2 θ = 2 b cos ⁡ θ s e n   θ

s = 2 b cot ⁡ θ

Resposta

E = m u 2 s e n 2 θ e b

s = 2 b cot ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo da trajetória parabólica y = b x 2 . Se sua componente da velocidade ao longo do eixo y é v y = c t 2 , determine as componentes x e y da aceleração da partícula. Aqui,
Uma partícula desloca-se ao longo da trajetória circular x 2 + y 2 = r 2 . Se a componente y da velocidade da partícula é v y = 2 r c o s 2 t , determine as componentes x e y da sua aceleração em qual
O jogador de beisebol A rebate a bola com v A = 12m / s e θ A = 60 ° . Quando a bola está diretamente acima do jogador B, ele começa a correr embaixo dela. Determine a velocidade escalar constante v B
Um garoto joga no ar uma bola a partir de O com uma velocidade v 0 em um ângulo θ 1 . Se ele em seguida joga outra bola com a mesma velocidade v 0 a um ângulo θ 2θ 1 , determine o tempo entre os lança
Uma bola de golfe é batida em A com uma velocidade de v A = 40m / s e direcionada em um ângulo de 30 ° com a horizontal como mostrado. Determine a distância d percorrida pela bola até atingir B.