Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 82
Para a viga e carregamento mostrados, (a) calcule o trabalho das forças quando elas são aplicadas sucessivamente à viga, usando o apêndice (b) calcule a energia de deformação da viga pelo método da seção e mostre que ela é igual ao trabalho obtido na parte
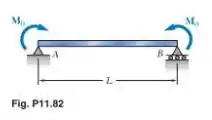
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Neste caso, usando o apêndice (caso 7):
Devemos traçar os gráficos de força por deslocamento dos dois casos. Eles serão:
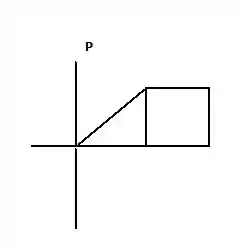
Para o primeiro caso, teremos:
Como
Passo 2
Para a letra b:
Sabemos que:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Os torques mostrados são exercidos nas polias A , B e C . Sabe-se que ambos os eixos são maciços e feitos de latão G = 39G P a , determinar a energia de deformação no: a eixo A B ; b eixo B C .
O eixo maciço de aço mostrado está submetido aos torques de 0,9k N × m , aplicados nas extremidades A e D . Usando G = 77G P a , determinar a energia de deformação do eixo.
Para o estado de tensões mostrado na Fig. a, determinar as tensões sobre um elemento orientado como mostrado na Fig. b. Calcular a densidade de energia de deformação específica, inicialmente dado pelo
Mostrar, por integração, que a energia de deformação da barra A B , em forma de tronco de cone, é U = 7 24 T 2 L G J m í n í onde J m í n í é o momento de inércia polar da seção transversal da barra,
Um cilindro vazado de borracha liga uma barra A , de raio R 1 , a um tubo B , de raio interno R 2 , formando um suporte isolante de vibração. Denotando por G o módulo de elasticidade transversal da bo