Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 199
Determinar a velocidade escalar do elevador se cada motor recolher o cabo a uma velocidade constante de 5m/s.
Passo 1
Verificando apenas o conjunto de cordas e polias envolvidas no sistema podemos dividir o comprimento total das cordas L em dois comprimentos L1 e L2. onde:
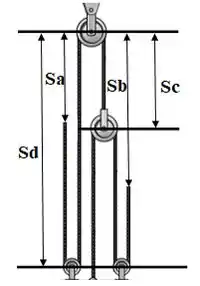
Onde:
(1)
E,
2
(2)
Passo 2
Somando as equações (1) e (2), temos.
(3)
Podemos assim, derivar a eq. (3), sabendo que r, L1 e L2 são comprimentos constantes:
Passo 3
Subistituindo o valor de va por 5m/s, e de vb também por 5m/s na equação encontrada, temos:
Resposta
Quando os motores A e B puxam os cabos com velocidades constantes, iguais a 5m/s cada, o elevador irá subir a uma velocidade escalar de vd de 2,14m/s.
Exercícios de Livros Relacionados
O homem puxa o garoto para cima do galho da árvore C ao caminhar para trás. Se ele parte do repouso quando xA= 0 e se desloca para trás com uma aceleração constante aA= 0,2 m/s2, determine a velocidad
O carro está se deslocando a uma velocidade escalar constante de 100 km/h. Se a chuva está caindo a 6 m/s na direção mostrada, determine a velocidade da chuva tendo como referência o motorista.
O homem consegue remar o barco na água parada com uma velocidade escalar de 5 m/s. Se o rio esta fluindo a 2 m/s, determine a velocidade escalar do barco e o ângulo θ que ele deve direcionar o barco d
O navio move-se com uma velocidade escalar constante vs = 20 m/s e o vento está soprando a uma velocidade escalar vW = 10 m/s, como mostrado. Determine a intensidade e direção da componente horizontal
No instante mostrado, os carros A e B movem-se a velocidades escalares de 30 km/h e 20 km/h, respectivamente. Se B está aumentando a sua velocidade escalar na razão de 1200 km/h2, enquanto A mantém um