Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 43
Determine a altura h do cone em termos do raio r do hemisfério , de modo que o conjunto esteja em equilíbrio indiferente. Tanto o cone como o hemisfério são feitos do mesmo material.
Passo 1
Desenhando o diagrama do corpo livre do cone+hemisfério:
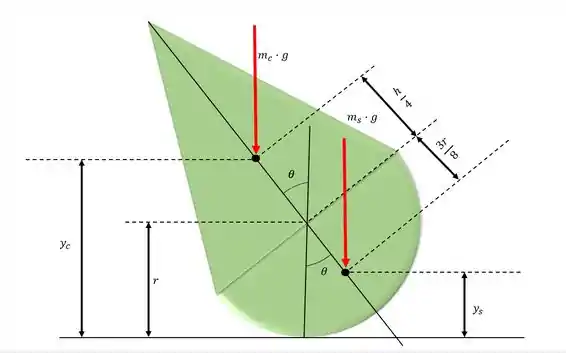
Passo 2
Em primeiro lugar vamos calcular a massa do cone e a massa do hemisfério em termos da massa específica:
Passo 3
Da figura, temos:
Passo 4
Vamos calcular a função para a energia potencial do conjunto:
Passo 5
Para calcular a posição de equilíbrio, devemos calcular a primeira derivada da função potencial:
Passo 6
Analisando a estabilidade, precisamos calcular a segunda derivada da expressão do potencial:
Resposta
Logo, o valor de h que proporciona estabilidade indiferente é
Exercícios de Livros Relacionados
Desprezando o peso dos blocos, determine 3 posições de equilíbrio para W = 1350 N ,l = 400 m m e k = 13,5 k N / m m
Sabendo que a mola está indeformada quando θ = 0 , dado P = 135 N ,a = 100 m m ,b = 75 m m ,r = 150 m mek = 0,9 k N / m d e t e r m i n e dois valores de θ para equilíbrio e determine a estabilidade p
Sabendo que a mola está indeformada quando y = 0 , determine o valor de y para equilíbrio quando W = 80 N ,l = 500 m m e k = 600 N / m m .
Usando o método da seção 10.8, resolva o probelma 10.34.
Resolva o Problema 10.97 sabendo que l = 800m m e k = 2,5k N / m .