Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 39

Uma ligação uniforme AB tem massa de 3 kg e está conectada nas duas extremidades por meio de pinos. A barra BD, com peso desprezível, passa por um bloco giratório em C. Se a mola tem uma rigidez k = 100   N / m e está livre quando θ = 0 º . Determine o ângulo θ para o equilíbrio e investigue a estabilidade na posição de equilíbrio. Despreze o tamanho do bloco giratório.

Passo 1

Desenhando o diagrama do corpo livre:

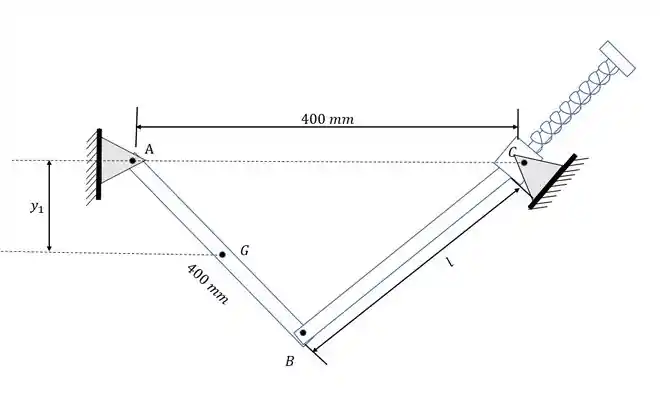
Passo 2

Da geometria da figura, vemos que:

y 1 = 200 1000 ⋅ s e n θ = 0,2   s e n θ y 1 = 0,2 s e n θ

Para encontrarmos o tamanho BC podemos utilizar a lei dos cossenos. Relembrando:

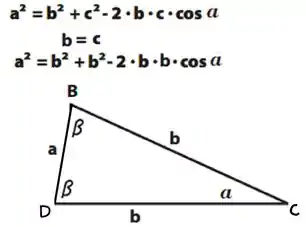
l 2 = A B 2 + A C 2 - 2 × A B × A C × c o s θ l 2 = 0,4 2 + 0,4 2 - 2 × 0,4 × 0,4 × c o s θ l 2 = 0,32 - 0,32 c o s θ l = √ ( 0,32 - 0,32 c o s θ )

Passo 3

Calculando as energias potenciais individuais da ligação AB e da mola tomando o eixo y para cima da linha AC:

Ligação AB:

V g = - m g y 1 V g = - 3 × 9,81 × 0,2 s e n θ = - 5,886 s e n θ

Mola:

V s = 1 2 k s 2 = 1 2 × 100 × 0,32 - 0,32 c o s θ = 16 ( 1 - c o s θ )

Passo 4

Calculando a energia potencial total do sistema temos:

V = V g + V s V = - 5,886 s e n θ + 16 1 - c o s θ

Passo 5

Para encontrar a posição de equilíbrio, devemos encontrar a primeira derivada:

d V d θ = d d θ   - 5,886 s e n θ + 16 1 - c o s θ   d V d θ =   - 5,886 c o s θ + 16 s e n θ d V d θ = 0 ⇒ 16 s e n θ = 5,886 c o s θ s e n θ c o s θ = tan ⁡ θ = 5,886 16 = 0,367 ⇒ θ = arctan ⁡ 20,15 º

Passo 6

Para analisar a estabilidade, devemos calcular a expressão da segunda derivada: d 2 V d θ 2 = d V d θ - 5,886 c o s θ + 16 s e n θ = 5,886 s e n θ + 16 s e n θ d 2 V d θ 2 θ = 20,15 º = 5,886 × sen ⁡ 20,15 º + 16 cos ⁡ 20,15 º = 17,04   ⇒   e s s t á v e l

Resposta

θ = 20,15   ( e s t á v e l )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da seção 10.8, resolva o probelma 10.38.
Determine o valor de θ para equilíbrio e a estabilidade deste. Despreze o atrito nas correias e considere as barras com massa m e nto l .
Se a mola está indeformada quando seu comprimento vale o raio r , determine o valor do ângulo para equilíbrio se W = 225 N ,r = 225 m m ek = 2,7 k N / m .
Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 30 .
Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 6 0 .