Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 207
A seção transversal monstrada representa um corpo de revolução, em torno do eixo , de uma peça fabricada em ferro fundido. Calcule sua massa .
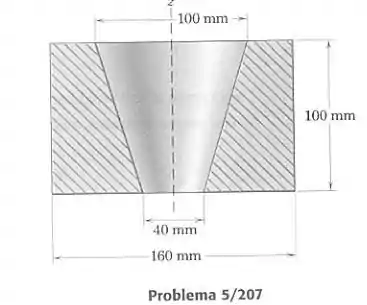
Passo 1
Vamos calcular o volume do corpo de revolução através da seguinte relação:
Onde é a área da região que é revolucionada (apenas de um lado) e é a distância do centroide da área até o eixo de revolução, no caso o eixo . Então multiplicamos o volume pela densidade do ferro fundido e achamos a massa.
Passo 2
Para calcular , primeiro separamos nossa área em duas regiões:
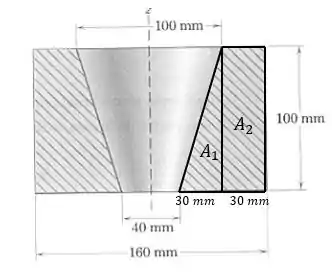
A primeira região tem área:
A distância do centroide para a base de um triângulo é um terço da altura relativa a essa base. Pegando a base vertical do triângulo, a altura relativa a essa base é 30 mm. A distância do centroide até essa base vertical é então de 10 mm (da direita para a esquerda). Então:
Então o volume da primeira região pode ser calculado:
Passo 3
A segunda região tem área:
E as coordenada do centroide é:
Então obtemos seu volume:
Passo 4
Temos então nosso volume total:
A densidade do ferro é de , então: