Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 80

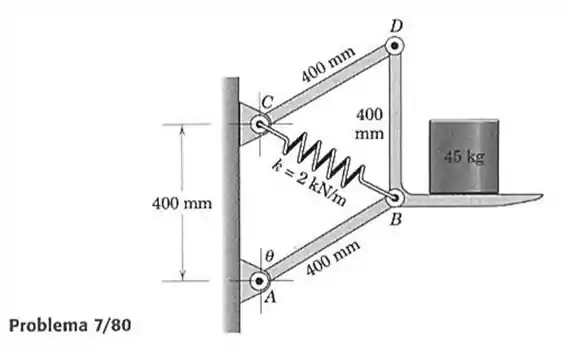
80- Determine o ângulo de equilíbrio θ para o mecanismo mostrado. A mola de rigidez k = 2 k N / m tem um comprimento de 200   m m quando não está esticada. Cada uma das conexões uniformes A B   e C D tem uma massa de 4.5   k g e o elemento B D , com sua carga, tem uma massa de 45   k g . Os movimentos ocorrem no plano vertical.

Passo 1

Como foi nos dado o comprimento inicial da mola vamos calcular qual seria o comprimento final em função de θ .

Podemos dividir o triângulo A C B em dois triângulos retângulos de modo sejamos capazes de encontrar o tamanho l f da mola com os comprimentos desses lados.

Fazendo seno e cosseno do ângulo θ teremos:

sin ⁡ θ = d 0.4 → d = 0.4 sin ⁡ θ

cos ⁡ θ = c 0.4 → c = 0.4 cos ⁡ θ

Como e + c = 0.4 temos o comprimento de e :

e = 0.4 - c = 0.4 - 0.4 cos ⁡ θ = 0.4 ( 1 - cos ⁡ θ )

Logo o tamanho l f da mola será por Pitágoras:

l f 2 = e 2 + d 2 = 0.4 2 ( 1 - cos ⁡ θ ) 2 + 0.4 2 sin 2 ⁡ θ

l f 2 = 0.4 2 2 - 2 c o s θ = 2 × 0.4 2 ( 1 - cos ⁡ θ )

l f = 0.32 ( 1 - cos ⁡ θ ) = 0.566 1 - cos ⁡ θ

Como l 0 = 0.2   m a deformação na mola será:

Δ x = l f - l 0 = 0.566 1 - cos ⁡ θ - 0.2

Δ x = 0.2 ( 2.83 1 - cos ⁡ θ - 1 )

Com 1 - cos ⁡ θ = 2 sin 2 ⁡ θ 2 logo:

Δ x = 0.2 2.83 2 sin 2 ⁡ θ 2 - 1 = 0.2 4 sin 2 ⁡ θ 2 - 1

Logo a energia potencial do elástica do sistema será:

Para k = 2000   N / m

V e = k 2   Δ x 2 = 1000 × 0.2 4 sin 2 ⁡ θ 2 - 1 2 = 200 4 sin 2 ⁡ θ 2 - 1 2

Passo 2

Para encontrar a energia potencial gravitacional do sistema precisaremos fazer uso do desenho base abaixo:

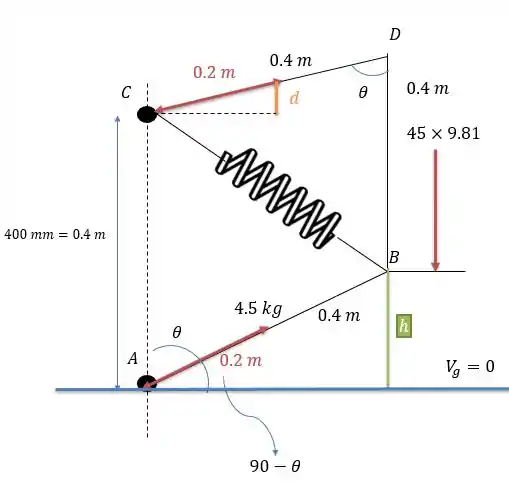
Vamos calcular a energia de cada barra separadamente e depois juntar-la:

A barra D B tem uma massa total de 45 kg (barra mais a carga) e está situada a uma altura h do ponto de eixo nulo, que pode ser calculado como:

sin ⁡ 90 - θ = h 0.4

Mas como sin ⁡ 90 - θ = cos ⁡ θ teremos:

h = 0.4 cos ⁡ θ

Logo a energia potencial gravitacional desse sistema será:

V g D B = 45 × 9.81 × 0.4 cos ⁡ θ = 176.58 cos ⁡ θ

A energia gravitacional da barra A B   será o rebatimento do seu centro de massa na vertical que será:

V g A B = 4.5 × 9.81 × 0.2 cos ⁡ θ = 88.29 cos ⁡ θ

Já da barra C D é a soma da altura de 0.4m com o rebatimento vertical de seu centro de massa que será:

V g C D = 4.5 × 9.81 × ( 0.4 + d )

Onde d é obtida por:

cos ⁡ θ = d 0.2 → d = 0.2 cos ⁡ θ

Uma vez que o ângulo C D B é o mesmo que o ângulo C A B e inicialmente B D é paralelo a vertical.

V g C D = 441.45 ( 0.4 + 0.2 cos ⁡ θ ) = 176.58 + 88.29 cos ⁡ θ

Somando todas as energias gravitacionais temos:

V g = 353.16 cos ⁡ θ + 176.58

Somando agora com a energia potencial elástica teremos uma energia potencial total a:

V = 200 4 sin 2 ⁡ θ 2 - 1 2 + 353.16 cos ⁡ θ + 176.58

Passo 3

Se derivarmos essa equação em relação a θ nós teremos:

d V d θ = 6400 sin 3 ⁡ x 2 cos ⁡ x 2 - 1153.16 sin ⁡ x

Se plotarmos o gráfico disso e quisermos encontrar quando é zero nós encontraremos o valor de θ = 73.783   ° para o equilíbrio.

Resposta

θ = 73.783 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19. A mola está livre quando θ = 45 ° e tem uma rigidez k = 20k N / m . Determine o ângulo θ para equilíbrio se cada um dos cilindros pesa 250N . Despreze o peso dos membros. A mola permanece horizont
12. Resolva o Problema 11.11 se a força P for aplicada verticalmente para baixo no ponto B .
17.Uma mesa de servi uniforme de 5k g está apoiada em cada lado por dois pares de ligação, A B e C D , e molas C E . Se a tigela tem massa 1k g e está em equilíbrio quando θ = 45 ° , determine a rigid
16. Uma mesa de servi uniforme de 5k g está apoiada em cada lado por dois pares de ligação, A B e C D , e molas C E . Se a tigela tem massa 1k g , determine o ângulo θ onde a mesa está em equilíbrio.
15.A montagem é usada para exercício. Ela consiste em quatro barras conectadas por pinos, cada uma com extensão L e uma mola de rigidez k e comprimento livre a(2 L ) . Se forças horizontais são aplica