Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 14
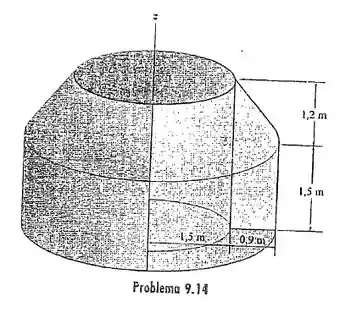
Determine a área de superfície e o volume do sólido formado girando-se a área sombreada em torno do eixo .
Passo 1
Falaa, querido!
O problema pede que encontremos a área de superfície e o volume do sólido de revolução. Lembre-se do Teorema de Pappus e Guldinus, se precisar de ajuda sobre esse teorema tem ótimas vídeo aulas aqui mesmo no Responde Aí, mas basicamente o teorema diz que:
A área de superfície é dada pela multiplicação da linha de que gera o sólido (curva de geração), pelo ângulo em radianos (no nosso caso ) e pela distância perpendicular do eixo de giração até o centroide da curva.
O volume do solido é dado pela multiplicação da aréa que gera o sólido pelo ângulo em radianos (no nosso caso ) e pela distância perpendicular do eixo de giração até o centroide da curva
Sendo a coordenada do centro de massa em relação ao eixo . Já que essa é a distância perpendicular do nosso centroide até o eixo de giração .
Bora!
Passo 2
Repara que nosso sólido é oco, então temos essa situação:
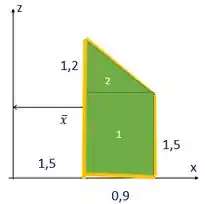
A curva de geração é do sólido é essa amarela. E a área de geração é essa verde. Vamos trabalhar para achar o volume primeiro.
A a área da figura que será rotacionada:
Passo 3
Agora, vamos calcular a coordenada do centro de massa da figura.
Temos uma figura composta. Você pode encontrar o centro de massa dessas figuras no final do livro. O centro de massa total vai ser a média ponderada (em relação a área de cada figura) entre esses centros:
Passo 4
Então agora usamos de fato o Teorema de Pappus e Guldinus:
Passo 5
Para área da superfície vamos dar uma mudada na fórmulinha do passo 1. Como a gente tem uma figura composta, nós vamos calcular:
Sendo o comprimento de uma linha de geração e a coordenada do centroide dessa linha.
Aqui difere do caso do volume porque lá nosso centroide era em relação às áreas e aqui é em relação as retas.
Bora calcular. Para a reta inclinada, o centroide é no meio da sua projeção em . Para as retas horizontais, o centroide é no meio delas. E para as retas verticais, o centroide é na sua coordenada . Fica assim: