Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 6

Localize o centroide z - do sólido homogêneo formado girando-se a área sombreada em torno do eixo z .

Passo 1

O nosso primeiro passo aqui é calcular o volume da região sombreada.

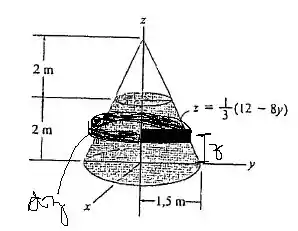
Um elemento com a forma de um disco fino foi escolhido. Esse elemento tem espessura d z , intercepta a curva de geração no ponto arbitrário 0 , y , z e, portanto, seu raio é r = y . Sabendo que o volume do elemento é d V = ( π y 2 ) d z e o seu centroide está localizado em z ~ = z :

z - = ∫ z d V ∫ d V

Vamos tratar primeiro a parte de cima da equação!

∫ z d V = ∫ 0 2 z π y 2 d z

Podemos escrever o y como:

z = 1 3 12 - 8 y

3 z - 12 = - 8 y

y = 1 8 ( 12 - 3 z )

Substituindo esse valor na integra, temos:

∫ 0 2 z π 1 8 ( 12 - 3 z ) 2 d z = π 6 4 ∫ 0 2 144 - 6 z + 9 z 2 z d z

= π 64 ∫ 0 2 ( 144 z - 72 z 2 + 9 z ³ ) d z

= π 64 144 z 2 2 - 72 z 3 3 + 9 z 4 4 0 2

= π 64 72 × 2 2 - 2 4 × 2 3 + 9 × 2 4 4

= 132 π 64 = 33 π 16

Passo 2

Nesse segundo momento, vamos calcular o valor para ∫ d V .

∫ d V = ∫ 0 2 π y 2 d z

∫ d V = π ∫ 0 2 ( 1 8 ( 12 - 3 z ) ) ²   d z

∫ d V = π 64 ∫ 0 2 144 - 72 z + 9 z 2 d z = π 6 4 144 z - 72 z 2 2 + 9 z 3 3 0 2

∫ d V = π 64 144 × 2 - 36 × 2 2 + 3 × 2 3

∫ d V = 168 π 64 = 42 π 16 = 21 π 8

Passo 3

Por último, vamos agora calcular o valor do y - !

z - = 33 π 16 21 π 8

z - = 33 π 16 ⋅ 8 21 π = 33 42 = 11 14

Resposta

O valor de z - é:

z - = 11 14

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.56. Determine the y-coordinate of the centroid of the shaded area.
5.55. Determine the x- and y-coordinates of the centroid of the shaded area.
5.63. Determine the coordinates of the mass center of the body constructed of a uniform square plate, a uniform straight rod, a uniform quarter-circular rod, and a particle (negligible dimensions). Th
Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.
Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.