Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 73
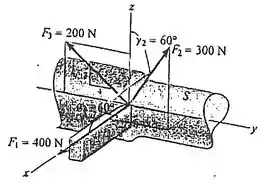
O eixo exerce três componentes de força sobre a ferramenta . Encontre a intensidade e os ângulos de direção coordenados da força resultante. A força atua dentro do octante mostrado.
Passo 1
Queremos encontrar a força , antes vamos decompor nossas forças do sistema.
Nossa já está praticamente pronta como se encontra sobre o eixo :
Passo 2
Para a já temos dois ângulos de direção coordenada, vamos encontrar o terceiro pela relação:
Assim:
Agora decompondo nas suas componentes:
Para :
Para :
E Para :
E o vetor cartesiano de fica:
Passo 3
Agora nossa , ela se encontra no plano , então terá duas componentes e vamos encontra-las usando a relação de catetos e hipotenusas do triângulo dado:
No eixo
No eixo :
Logo, nossa como vetor cartesiano:
Passo 4
Na nossa reta final, vamos encontrar a força resultante, dado que:
E a intensidade do seu módulo será:
Passo 5
Só falta encontrar os ângulos de direção coordenados de , sendo:
Então: