Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 13
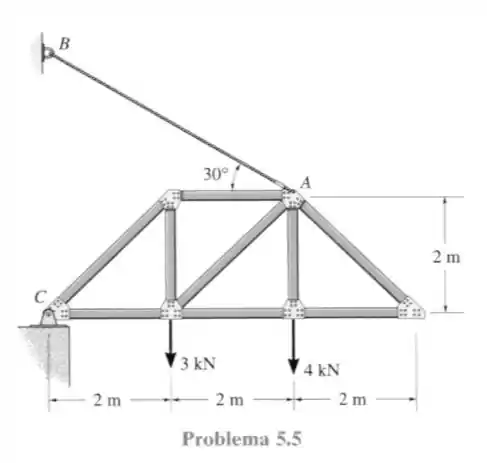
13. Determine as reações nos apoios da treliça no Problema .
Passo 1
O mais importante aqui, para determinar as reações nos apoios quando estamos falando de treliça, é ver a treliça como um corpo grandão em que as forças internas (entre as barras) não fazem diferença nenhuma para esse cálculo.
Então a gente vai basicamente somar todas as forças e momentos externos e igualar a zero, pois a treliça está estática.
Passo 2
Primeiro, vamos ver o diagrama de forças da nossa situação, para analisar as reações que teremos que determinar no nosso sistema e ficar mais simples de ver o que fazer.
Observe que em existem duas reações, uma vertical e outra horizontal. Além disso existe a força de tração no cabo
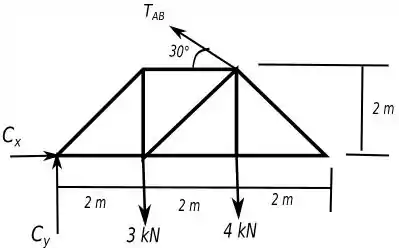
Então para achar as reações que o enunciado pede, teremos que usar as equações de equilíbrio.
Mas será mais conveniente calcular o momento em relação ao ponto , já que e , não interferem no cálculo e assim conseguiremos achar a tração logo de cara =D
Passo 3
Vamos então calcular o momento em relação a , para acharmos . Vamos considerar o sentido anti-horário como o positivo.
Mas qual é a distância ? Bom aqui a gente pode fazer de dois jeitos: decompor a distância ou decompor a força.
Aqui nós vamos decompor a força nas componentes vertical e horizontal:
Então vamos ter:
Lembrando que a gente tem que pegar a distância perpendicular à força, por isso pegamos a distância em e multiplicamos pela força em , ok? Temos:
Voltando à nossa equação:
Passo 4
Agora vamos analisar as equações de equilíbrio referentes a força primeiro na direção , depois na direção .
Agora para