Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 20
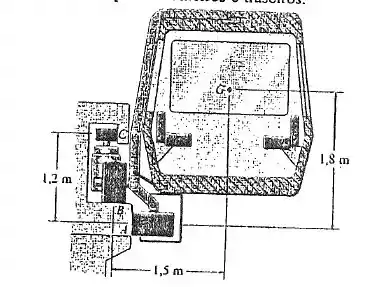
O vagão ferroviário possui um peso de e centro de gravidade em . Ele é suspenso pela frente e por trás no trilho por seis pneus localizados em . Determine as reações normais desses pneus se considerarmos que o trilho é uma superfície lisa e uma parte igual da carga é sustentada nos pneus dianteiros e traseiros.
Passo 1
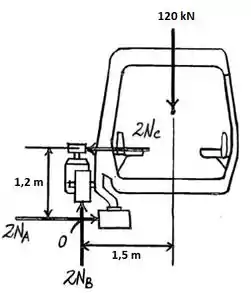
Bom pessoal, nós temos seis pneus que tocam nesse vagão, certo? Cada pneu terá sua normal de reação. Se em cada ponto temos dois pneus, então o total da normal será, em cada ponto, . Vamos colocar, também, o ponto , entre e , como nossa referência para os cálculos. Assim, o desenho para essa situação fica:
Passo 2
Vamos calcular o momento em relação a para encontrarmos o valor da componente . e não entram nessa conta pois são forças que estão atuando no ponto , possuindo distância zero até ele. Assumindo que o sentido anti-horário é positivo para o momento, temos:
Passo 3
Nos restou encontrar e agora. Para isso, vamos analisar as forças que atuam na horizontal e na vertical. Primeiramente vamos para a horizontal, ok? Numa situação de equilíbrio, a soma de todas as forças que atuam na horizontal tem que ser zero. Vamos assumir a direção para direita como positiva. Assim,
Passo 4
Vamos agora ver o resultante vertical. Numa situação de equilíbrio, a soma de todas as forças que atuam na vertical tem que ser zero. Vamos assumir a direção para cima como positiva. Logo,
Resposta
Os valores para as componentes de reação são: