Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 83
Determine o momento de binário resultante dos dois binários que agem sobre o encanamento. A distância de a é . Expresse o resultado como um vetor cartesiano.
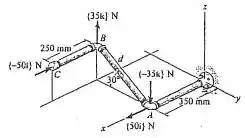
Passo 1
A questão pede o binário resultante de dois binários que agem sobre o encanamento. A fórmula para um binário de duas forças antiparalelas separadas por um vetor é
Assim, temos que calcular cada um dos binários e somá-los vetorialmente. Para uma das forças, o vetor distância é dado por
Já para a outra força,
Usaremos e .
Passo 2
Calculando os produtos vetoriais:
Portanto,
Passo 3
Substituindo , e , temos que
Assim,
Resposta
Exercícios de Livros Relacionados
A força trativa T no cabo A B é mantida em um valor constante de 120 N. Determine o momento M O dessa força trativa em torno do ponto O na faixa 0 ° ≤ θ ≤ 90 ° . Faça um gráfico das componentes x , y
A força F está direcionada de A para D e D pode se movimentar de B até C , sendo sua posição medida pela variável s . Considere a projeção de F sobre a linha E F como função de s . Em particular, dete
O braço A B gira na faixa 0 ° ≤ θ ≤ 180 ° , e a mola não está esticada quando θ = 90 ° . Determine, em função de θ , o momento em torno de O causado pela força aplicada pela mola em B . Faça um gráfic
142. O cabo A B exerce uma força de 80N sobre a extremidade da barra de 3m de comprimento O A . Determine a intensidade da projeção dessa força ao longo da barra.
Determine o momento de binário que age sobre o encanamento e expresse o resultado como um vetor cartesiano.