Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 55
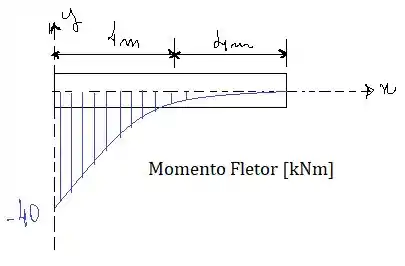
Determine os diagramas de esforço cortante e de momento fletor para a viga.
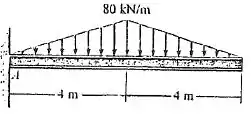
Passo 1
Vamos desenhar o diagrama de corpo livre da viga, beleza?
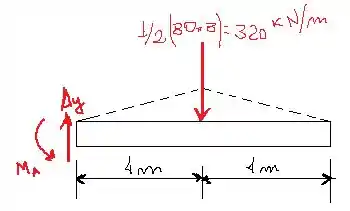
Antes de encontrarmos os valores do esforço cortante e momento fletor, vamos encontrar as reações de apoio através do diagrama de corpo livre desenhada acima. Assim,
Passo 2
Vamos agora olhar para a porção que compreende o intervalor .
Bom, devido aos triângulso proporcionais, a carga distribuída que atuam no final deste segmento tem uma intensidade ou . Ela vai ser substituída por uma força resultante é igual a . Essa força atua no centroide da área da carga distribuída, que fica a uma distância de da extremidade direita.
Vamos aplicar as equações de equilíbrio no diagrama de corpo libre para determinarmos a força cortante e o momento fletor .
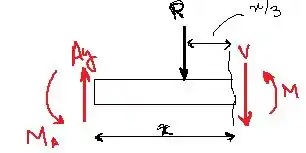
Passo 3
Vamos agora olhar para a porção que compreende o intervalor .
Bom, devido aos triângulso proporcionais, a carga distribuída que atuam no final deste segmento tem uma intensidade ou . Ela vai ser substituída por uma força resultante é igual a . Essa força atua no centroide da área da carga distribuída, que fica a uma distância de da extremidade direita.
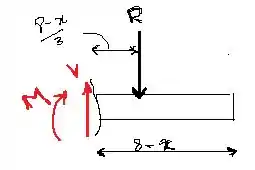
Vamos aplicar as equações de equilíbrio no diagrama de corpo libre para determinarmos a força cortante e o momento fletor .
Passo 4
Vamos agora plotar os diagramas de esforço cortante e momento fletor. A função de esforço cortante varia conforme as expressões que encontramos no passo anterior. Logo, o diagrama de esforço cortante se torna:
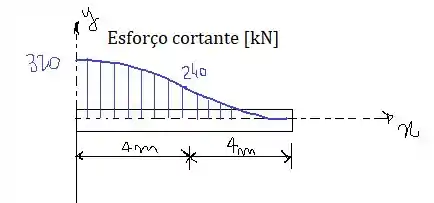
A função do momento fletor tem um diagrama igual a:
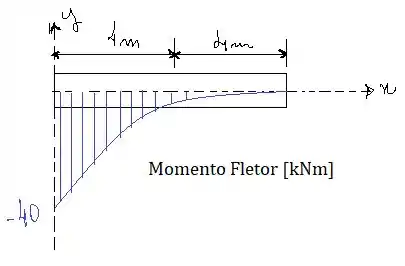
Resposta
