Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 56

Se o momento combinado das duas forças em relação ao ponto é zero, determine:

(a) o módulo da força ;

(b) o módulo da resultante das duas forças;

(c) as coordenadas e do ponto sobre a periferia da roda, em relação ao qual o momento combinado das duas forças é máximo;

(d) o momento combinado das duas forças em relação a .

Passo 1

Vamos chamar de a resultante entre as forças e a de . Se essa resultante produz momento nulo em relação a , essa força precisa ser paralela à linha que une ao ponto de ação dessa força.

Isso vai render um desenho bem complicado (e fora de escala), mas vamos lá:

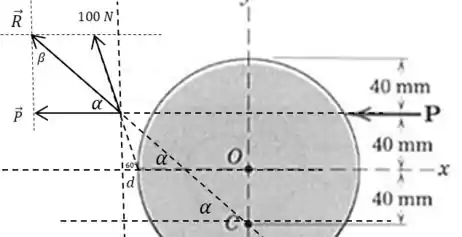
Perceba que o primeiro paso desse desenho foi desenhar uma linha que passa pelo ponto contendo a resultante das duas forças.

Precisamos encontrar aqueles dois ângulos e . Vamos calcular a tangente de olhando para o ponto onde ele está mais próximo de :

E também podemos calcular :

Então:

E como a soma dos ângulos internos de um triângulo precisa ser igual a :

Passo 2

(a) Agora podemos usar a lei dos senos para encontrar a força :

Passo 3

(b) E fazendo a mesma coisa para a força resultante :

Passo 4

(c) O ponto em relação ao qual o momento das duas forças é máximo é aquele que está na reta perpendicular à direção da força resultante. Vamos reformular o desenho, mostrando como podemos chegar em uma expressão para essa coordenada:

Esse monte de linhas apareceu para mostrarmos como aquele ângulo foi parar ali! Como o raio do círculo é :

Passo 5

(d) Por último queremos saber qual é o momento combinado das duas forças em relação a esse ponto cujas coordenadas nós acabamos de calcular.

Bom, nós já vimos que o módulo da força resultante é:

Agora só precisamos multiplicar isso pela distância entre a linha de ação dessa força e o ponto . Olhando para a figura acima dá pra ver que essa distância resulta na seguinte expressão:

E esse momento age no sentido horário.

Resposta

(a)

(b)

(d) (sentido horário)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para levantar o mastro O C , uma armação leve O A B é presa ao mastro e uma força trativa de 3,2k N é aplicada ao cabo de sustentação pelo guincho em D . Calcule o momento M O desta força trativa em r

Um puxão T de 150N é dado em uma corda, que está firmemente enrolada na parte interna do tambor. Determine o momento de T em relação ao centro do tambor em C . Em que ângulo θ , T deve ser aplicado de

Elementos do braço são mostrados na figura. A massa do antebraço é de 2,3k g , com centro de massa em G . Determine o momento combinado em relação ao cotovelo em O dos pesos do antebraço e da esfera h

A força de 10N é aplicada sobre a manopla da válvula de controle hidráulico, como mostrado. Calcule o momento dessa força em relação ao ponto O .

Um praticante de exercício começa com seu braço na posição relaxada O A , na qual a fita elástica não está esticada. Ele então gira seu braço para a posição horizontal O B . O módulo elástico da fita