Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 19
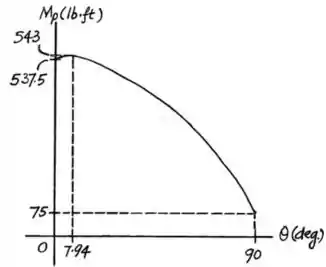
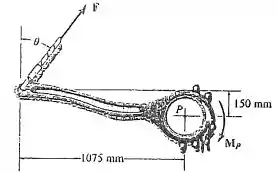
As pinças são usadas para prender as extremidades do tubo de perfuração . Determine o torque (momento) que a força apliada exerce sobre o tubo em relação ao ponto como uma função de . Represente graficamente esse momento em função de para .
Passo 1
Para determinar o momento gerado pela força é necessário determinar as distâncias do ponto até os pontos de atuação da força e aplicar o princípio do momento.
Passo 2
Dessa forma, supondo que o momento positivo atue no sentido horário, tem-se que:
Passo 3
Um ponto que pode ser definido para ser plotado no gráfico é o ângulo para obter o momento máximo:
Rearranjando esta equação:
Assim,
Resposta
Exercícios de Livros Relacionados
Determine o momento da força em relação ao ponto O .
Determine o momento da força em relação ao ponto O .
Determine o momento da força em relação ao ponto O .
Determine o momento resultante produzido pelas forças em relação ao ponto O .
Determine o momento da força em relação ao ponto O .