Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 55
Determine a distancia desde o fundo da placa da base até o centroide da seção estrutural mostrada.
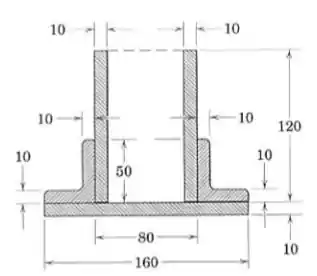
Passo 1
Sabendo que as equações para encontrar o centroide é dado por:
Mas graças aos deuses da mecânica, este problema é simétrico!! Dessa maneira, vamos primeiro encontrar a área do problema, em forma de tabela, considerando somente a direção vertical, no caso, !!
Passo 2
Primeiro vamos definir nossos elementos de área, nosso problema fica muito mais fácil de dividirmos em várias áreas e calcularmos a soma de cada uma!
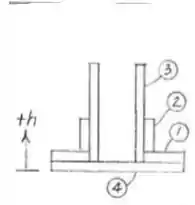
Assim ficando cada área definida acima!!
Passo 3
Vamos então, definir o que é cada área de cada problema!
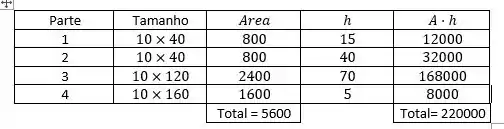
Passo 4
Agora fica bem simples gente, porque podemos voltar para nossa formula original de centroide a partir de área sem integral:
Resposta
Exercícios de Livros Relacionados
Localize o centroide da área da seção transversal do canal.
Localize o centroide do fio. Se o fio for suspenso por A , determine o ângulo que o segmento A B faz com a vertical quando o fio está em equilíbrio.
Localize o centroide da área composta.
Localize o centroide do fio que está dobrado na forma mostrada.
Encontre o centroide do fio.