Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 33

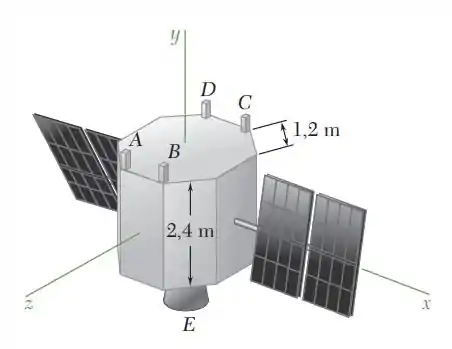
18.33. Uma sonda de 2.500 kg em órbita ao redor da Lua tem 2,4 m de altura e bases octogonais com lados de 1,2 m. Os eixos de coordenadas mostrados na figura são os eixos centroidais principais de inércia da sonda e seus raios de giração são kx 0,98 m, ky 1,06 m e kz 1,02 m. A sonda é equipada com um propulsor principal de 500 N de empuxo E e com quatro propulsores de 20 N de empuxo A, B, C e D que podem expelir propelente no sentido y positivo. A sonda tem uma velocidade angular (0,040 rad /s)i (0,060 rad /s)k quando dois dos propulsores de 20 N são usados para reduzir a velocidade angular a zero. Determine (a) quais dos propulsores devem ser usados, (b) o tempo de operação de cada um desses propulsores, (c) por quanto tempo o propulsor principal E deve ser ativado para que a velocidade do centro de massa da sonda permaneça inalterada.

Passo 1

Beleza vamos para mais um problema! E esse problema vai ser bem legal porque o enunciado vai ajudar a gente a calcular H → G rapidinho.

H → G = I x ω x   i ^ + I y ω y   j ^ + I z ω z   k ^

Isso fica

H → G = m k x 2 ω x   i ^ + k y 2 ω y + k z 2 ω z   k ^

A gente tem o valor de tudo nessa expressão, só substituir:

H → G = 2500 0,98 2 0,040   i ^ + 1,06 2 0 + 1,02 2 0,060   k ^

Fazendo essa continha

H → G = 96,04   i ^ + 156,06   k ^   k g ⋅ m 2 s

Viu como foi rapidinho? Mas calma, o problema não acabou ainda.

Passo 2

Vamos agora definir os propulsores do motor como:

A → = - A   j ^ B → = - B   j ^ C → = - C   j ^ D = - D j ^

Esses são os propulsores que tem o impulso de 20   N cada.

E → = E   j ^

Esse é o propulsor de 500   N .

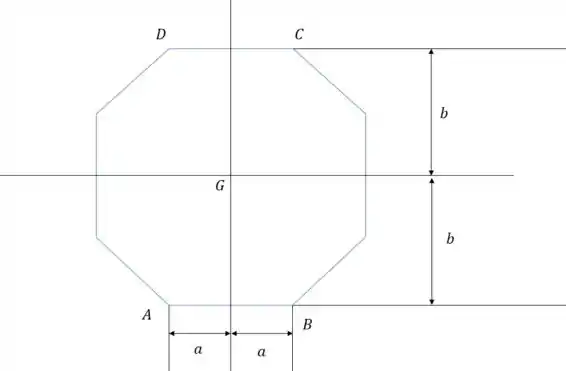
Essa é a vista de cima da sonda.

A gente já pode calcular os valores de a e b .

a = 1,2 2 = 0,6   m

E

b = a + a 2 + a 2 = 0,6 ⋅ 0,6 2 = 1,4485   m

Sabe porque calculamos essas distâncias? Porque agora podemos escrever o vetor posição de cada propulsor.

r → A = - a   i ^ + b   k ^ r → B = a   i ^ + b   k ^ r → C = a   i ^ - b   k ^ r → D = - a   i ^ - b   k ^

Passo 3

Agora vamos usar o princípio do impulso-momento.

H → G + r → A × A → + r → B × B → + r → C × C → + r → D × D → = 0

Já que o momento angular final e o momento linear final são nulos.

Olha só, a gente já calculou todos os vetores dessa equação. Para não ficar desorganizado vamos resolver tudo parte por parte:

r → A × A → = - a   i ^ + b   k ^ × - A   j ^ = b A   i ^ + a A k ^

r → B × B → = a   i ^ + b   k ^ × - B   j ^ = b B i ^ - a B   k ^

r → C × C → = a   i ^ - b   k ^ × - C j ^ = - b C   i ^ - a C   k ^

r → D × D → = - a   i ^ - b   k ^ × - D   j ^ = - b D   i ^ + a D   k ^

Então

H → G + b A   i ^ + a A k ^ + b B i ^ - a B   k ^ + - b C   i ^ - a C   k ^ + - b D   i ^ + a D   = 0

Ou simplificando

b A + B - C - D i ^ + a A - B - C + D k ^ = - H → G

Agora a melhor estratégia para a gente seguir é resolver por componentes:

A + B - C - D = - H G x b

Então

A + B - C - D = - 96,04 1,4485 = - 66,30   N ⋅ s

E

A - B - C + D = - H G z a

Então

A - B - C + D = - 156,06 0,6 = - 260,1   N ⋅ s

Passo 4

Beleza agora finalmente a gente pode ir pro item (a).

Dois propulsores devem estar ligados e dois desligados, bom se a gente somar as equações temos:

2 A - C = - 326,4   N ⋅ s

E se subtrairmos

2 B - D = 193,8

Então se A = 0 , obrigatoriamente o propulsor C tem que estar ligado, e se D = 0 o motor B tem que estar ligado, o porto é que os motores A e C não podem estar desligados ao mesmo tempo assim como os motores B e D .

Então podemos responder o item (a) dizendo para usar os mores C e B .

C = 326,4 2 = 163,2   N

E

B = 193,8 2 = 96,9   N

Passo 5

Agora vamos para o item (b). Podemos usar essa equação:

F C Δ t C = C

Ou

Δ t C = C F C

Substituindo os valores

Δ t C = 163,2 20 = 8,16   s

E para o motor B

Δ t B = B F B

Isso fica

Δ t B = 96,9 20 = 4,84   s

Passo 6

E estamos na última parte do problema. Bom, o momento linear final é nulo, então

E   j ^ - B   j ^ - C   j ^ = 0

Logo

E = B + C

Então

E = 96,9 + 163,2 = 260,1

Então podemos fazer

Δ t E = E F E = 260,1 500 = 0,520   s

E terminamos mais uma.

Resposta

a : B   e   C b : Δ t C = 8,16   s                 Δ t B = 4,84   s c : Δ t E = 0,520   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco de 10 onças mostrado gira a uma taxa ω 1 = 750 r p m , enquanto o eixo AB gira conforme mostrado com uma velocidade angulada ω 2 of 6 r a d / s . Determine as reações dinâmicas em A e B.
Para o sistema do Problema 18.99, mostre que (a) a reação dinâmica em D é independente do comprimento 2a do painel, (b) a razão M1 / M2 das magnitudes dos pares exercidos pelos motores em A e C, respe
A haste delgada AB é presa por uma manilha ao braço BCD, que gira com uma velocidade angular constante ω em torno da linha de centro de sua porção vertical CD Determine a magnitude da velocidade angul
Um disco de peso W = 10 b gira com uma velocidade angular ω 2 em relação ao braço ABC, que por sua vez gira com uma velocidade angular ω 1 em torno do eixo y. Sabendo que ω 1 = 5rad / s e ω 2 = 15rad
Uma esfera de alumínio sólido de raio de 3 pol. É soldada à extremidade de uma haste AB de 6 pol. De comprimento de massa desprezível, que é suportada por uma junta de esfera e encaixe em A. Sabendo q