Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 44
18.44. Determine a energia cinética da placa triangular do Problema 18.16
Passo 1
Vamos relembrar o problema 18.16. Temos uma placa triangular que tem uma massa de soldada num eixo vertical girando à .
E a energia cinética pode ser encontrada pela equação:
Como só tem componente em temos:
Passo 2
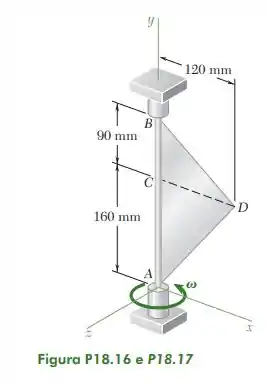
A placa é triangular, então para calcular seu momento de inércia precisamos saber a base e a altura desse triângulo. Essas informações estão na imagem do problema:
Então o momento de inércia de área é:
E consequentemente o momento de inércia da massa vai ser:
Isso fica
Então
Substituindo os valores
Passo 3
Então a energia cinética fica
Resposta
Exercícios de Livros Relacionados
O eixo do Problema 18.67 está inicialmente em repouso ( ω = 0), quando um binário de momento M0 é aplicado a ele. Sabendo que a resultante da aceleração angular é α = (20 rad/s2)i, determine (a) o bin
O conjunto do Problema 18.68 está inicialmente em repouso ( ω = 0), quando um binário de momento M0 é aplicado ao eixo AB. Sabendo que a aceleração angular resultante do conjunto é α = (150 rad/s2)i,
Uma haste delgada é dobrada para formar uma moldura quadrada de 6 pol. A estrutura é fixada por um colar em A a um eixo vertical que gira com velocidade angular constante 0. Determine (a) o ângulo β q
A lâmina de uma serra portátil e o rotor de seu motor têm massa total de 1,25 kg e raio de giração combinado de 40 mm. Sabendo que a lâmina gira do modo mostrado na figura a uma taxa ω 1 = 1.500 rpm,
Depois de prender a roda de 18 kg mostrada na figura a uma máquina de balanceamento e colocá-la para girar a uma taxa de 15 rev/s, um mecânico verifica que, para balancear a roda tanto estática como d