Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 51

Determine a equação da linha elástica. Especifique a deflexão em C

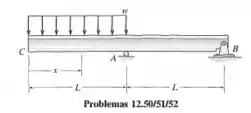
Passo 1

Começamos com as reações de apoio:

∑ M B = 0 ⇒ w ⋅ L ⋅ 3 L 2 - R A ⋅ L = 0

R A = 3 2 w L

∑ F Y = 0 ⇒ - w L + R A - R B = 0

R B = L 2

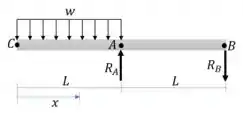
Passo 2

Para que possamos aplicar as equações de descontinuidade nesta viga, precisamos que o carregamento se estenda até o final da viga. Fazemos isso complementando o carregamento em cima, e aplicando um carregamento igual em sentido inverso para compensar:

Passo 3

Vamos utilizar o carregamento equivalente para calcular uma equação para o momento fletor:

M x = - w 2 < x - 0 > 2 + 3 2 w L < x - L > + w 2 < x - L > 2 - w L 2 < x - 2 L >

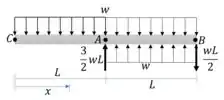
Podemos simplificar a expressão ignorando as forças que ficam na extremidade final da viga. Outra simplificação possível é: < x - 0 > n = x n se n > 0

A equação de momento fletor é:

M x = - w 2 x 2 + w 2 < x - L > 2 + 3 2 w L < x - L >

Passo 4

Vamos integrar uma vez para determinar a equação da inclinação

E I ⋅ θ = ∫ M x d x

E I ⋅ θ = ∫ - w 2 x 2 + w 2 < x - L > 2 + 3 2 w L < x - L > d x

E I ⋅ θ = - w 6 x 3 + w 6 < x - L > 3 + 3 4 w L < x - L > 2 + c 1

Passo 5

Vamos integrar mais uma vez para determinar a equação da linha elástica

E I ⋅ v = ∫ θ x d x

E I ⋅ v = ∫ - w 6 x 3 + w 6 < x - L > 3 + 3 4 w L < x - L > 2 + c 1 d x

E I ⋅ v = - w 24 x 4 + w 24 < x - L > 4 + 3 12 w L < x - L > 3 + c 1 x + c 2

Passo 6

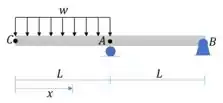
Pela tabela 12.1 podemos ver as condições de contorno para o apoio do ponto A:

x A = L

v A = 0

Aplicando na equação da linha elástica:

E I ⋅ v A = - w 24 x A 4 + w 24 < x A - L > 4 + 3 12 w L < x A - L > 3 + c 1 x A + c 2

0 = - w 24 L 4 + c 1 ⋅ L + c 2

c 1 ⋅ L + c 2 = 1 24 w L 4

Passo 7

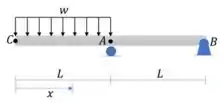
Pela tabela 12.1 podemos ver as condições de contorno para o apoio do ponto B:

x B = 2 L

v B = 0

Aplicando na equação da linha elástica:

E I ⋅ v B = - w 24 x B 4 + w 24 < x B - L > 4 + 3 12 w L < x B - L > 3 + c 1 x B + c 2

0 = - w 24 2 L 4 + w 24 L 4 + 3 12 w L 4 + 2 L c 1 + c 2

2 L c 1 + c 2 = 3 8 w L 4

Passo 8

Chegamos no sistema de equações:

c 1 L + c 2 = 1 24 w L 4

2 c 1 L + c 2 = 3 8 w L 4

Subtraíndo o primeiro do segundo:

c 1 L = 3 8 w L 4 - 1 24 w L 4

c 1 = 1 3 w L 3

Aplicando c 1   na primeira equação:

1 3 w L 3 ⋅ L + c 2 = 1 24 w L 4

c 2 = - 7 24 w L 4

Passo 9

As equações da inclinação e da deflexão são:

E I ⋅ θ = - 1 6 w x 3 + 1 6 w < x - L > 3 + 3 4 w L < x - L > 2 + 1 3 w L 3

E I ⋅ v = - 1 24 w x 4 + 1 24 w < x - L > 4 + 3 12 w L < x - L > 3 + 1 3 w L 3 ⋅ x - 7 24 w L 4

Passo 10

A posição do ponto C é:

x C = 0

A deflexão em C será:

E I ⋅ v C = - 1 24 w x C 4 + 1 24 w < x C - L > 4 + 3 12 w L < x C - L > 3 + 1 3 w L 3 ⋅ x C - 7 24 w L 4

E I ⋅ v C = - 1 24 w ⋅ 0 + 1 24 w ⋅ 0 + 3 12 w L ⋅ 0 + 1 3 w L 3 ⋅ 0 - 7 24 w L 4

v C = - 1 E I 7 24 w L 4

Resposta

E I ⋅ v = - 1 24 w x 4 + 1 24 w < x - L > 4 + 3 12 w L < x - L > 3 + 1 3 w L 3 ⋅ x - 7 24 w L 4

v C = - 1 E I 7 24 w L 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as reações nos apoios e a seguir trace os diagramas de força cortante e momento. EI é constante.
Determine as reações nos apoios A e B ; em seguida, trace os diagramas de força cortante e momento fletor. E I é constante. Despreze o efeito da carga axial.
A viga tem E 1 I 1 constante e é suportada pela parede fixa em B e pela haste AC. Se a haste tiver área de seção transversal A 2 e o material tiver módulo de elasticidade E 2 , determine a força na ha
Determine as reações ao momento nos apoios A e B. EI é constante.
Determine as reações nos apoios e, em seguida, trace os diagramas de força cortante e momento fletor. EI é constante.