Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 10
10. Determine o estado de tensão equivalente em um elemento se ele estiver orientado a 30° em sentido anti-horário em relação ao elemento mostrado. Use as equações de transformação de tensão.
Passo 1
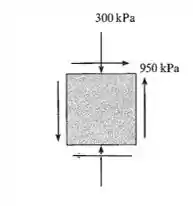
Olhando a figura acima, percebemos que trata-se de um estado plano de tensões, em que ocorre a seguinte situação:
, uma vez que não há nenhuma tensão normal na horizontal.
, com valor negativo uma vez que a tensão normal na vertical é de compressão.
, com valor positivo uma vez que as setas de tensão cisalhante apontam para o primeiro e terceiro quadrante.
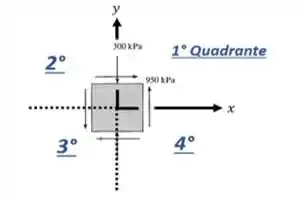
Se as setas de tensão cisalhante apontam para o primeiro e terceiro quadrante, tem valor positivo. Do contrário, se as setas apontam para o segundo e quarto quadrante, tem um valor negativo.
Passo 2
Bom! Chega de papo! Vamos fazer o que o exercício quer e determinar o estado de tensão , e no elemento do enunciado caso os seus eixos sejam rotacionados por um ângulo em sentido anti-horário. E se falou anti-horário, já dá pra saber que o nosso ângulo é positivo.
Agora, basta apenas aplicar as fórmulas de transformação de tensão que já conhecemos, para encontrar nossas novas tensões. São elas:
E sabemos também o valor das seguintes variáveis:
Só nos resta, então, substituir esses valores nas três expressões das tensões acima, para encontrar quanta vale cada uma.
E alcançamos os seguintes resultados:
Passo 3
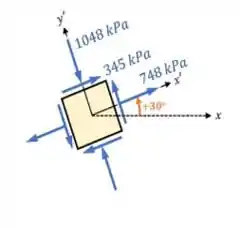
No passo anterior, já encontramos as respostas do nosso exercício, mas para complementar nossa solução, podemos desenhar essas mesmas tensões no nosso elemento rotacionado.
Sabemos que as tensões e , por serem positivas, vão ter os mesmo sentidos que tinham no estado plano da figura do enunciado, sendo representadas de maneira convencional. Já , que tem um valor negativo, vai ser representada com uma tensão compressiva.
Chegamos então, até a seguinte imagem:
