Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 45
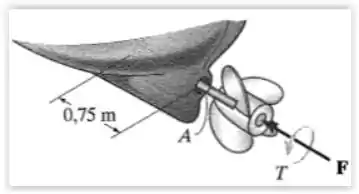
O eixo maciço da hélice de um navio estende-se para fora do casco. Em operação, ele gira a quando o motor desenvolve de potência, o que causa um impulso de no eixo. Se o diâmetro externo do eixo for , determine as tensões principais em qualquer ponto localizado na superfície do eixo.
Passo 1
Primeiro, vamos montar o diagrama de forças atuantes no eixo:
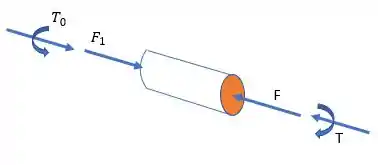
Como a força F é a força do impulso causado pelo motor e é a única força presente no pra compensar F, elas tem o mesmo módulo.
Para achar o torque , devemos calcular o torque , que no final das contas é a mesma coisa. Mas como o exercício deu a velocidade angular e a potência que o motor desenvolve, a gente pode achar bem fácil o que queremos, pela fórmula:
Passo 2
Agora, é só acharmos a tensão no eixo pela fórmula:
E também, calculemos a tensão máxima de cisalhamento eixo dada por:
Lembrando que o momento polar de inércia da seção transversal de um cilindro é dado pela fórmula , chegamos à:
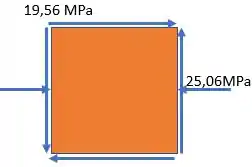
Passo 3
Com isso, a gente já consegue achar a tensão de cisalhamento máxima no plano em qualquer ponto da superfície pela já manjada, fórmula abaixo:
Resposta
Assim, a tensão máxima de cisalhamento no plano em qualquer ponto da superfície do eixo é: