Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 19

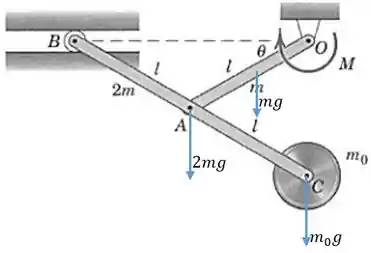
Determine o momento M que deve ser aplicado em O para sustentar o mecanismo na posição θ = 30 ° . As massas do disco em C , da barra O A e da barra B C   são m 0 , m e 2 m , respectivamente.

Passo 1

Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual δ U total realizado pelas forças externas ativas para um deslocamento pequeno do sistema deve ser zero:

δ U = 0

Os nossos agentes externos ativos (que realizam trabalho em um deslocamento do sistema) são: O peso m 0 g do disco, o peso m g da barra O A , o peso 2 m g da barra B C e o momento M . A força de apoio em O não pode realizar trabalho, pois esse ponto não se move. A força em B também não pode realizar trabalho, pois a força é vertical e o deslocamento nesse apoio só pode ser horizontal. Então devemos relacionar o trabalho infinitesimal causado pelos pesos e pelo momento com o ângulo θ , e então igualar o trabalho total a zero.

Passo 2

Primeiro vamos calcular o trabalho virtual δ U 1 causado pelos pesos das barras e do disco. A distância vertical do centro barra B C até a linha B O é:

y B C = l sen ⁡ θ

Então, derivando, a variação da altura é dada por:

δ y B C = l cos ⁡ θ δ θ

A altura y O A do centro da barra O A é dada por:

y O A = l 2 sen ⁡ θ

Então sua variação é:

δ y O A = l 2 cos ⁡ θ δ θ

Por último, temos a altura do centro do disco:

y C = 2 l sen ⁡ θ

Que possui variação em função de δ θ :

δ y C = l cos ⁡ θ δ θ

O trabalho virtual total realizado pelos três pesos para uma variação δ θ será a soma dos pesos vezes os deslocamentos:

δ U 1 = 2 m g   δ y B C + m g   δ y O A + m 0 g   δ y C

= 2 m g l cos ⁡ θ δ θ + m g l 2 cos ⁡ θ δ θ + m 0 g 2 l cos ⁡ θ δ θ

= 2 m g l cos ⁡ θ δ θ + m g l 2 cos ⁡ θ δ θ + 2 m 0 g l cos ⁡ θ δ θ

⇒ δ U 1 = 5 m 2 + 2 m 0 g l cos ⁡ θ δ θ

Passo 3

Agora calculamos o trabalho virtual δ U 2 causado pelo momento. Para um aumento δ θ a barra O A irá girar um ângulo de δ θ no sentido anti-horário, sentido contrário ao do momento. Então, temos o trabalho na barra O A , que é negativo:

δ U 2 = - M δ θ

Passo 4

Então aplicamos o Princípio do Trabalho virtual:

δ U = δ U 1 + δ U 2 = 0

⇒ 5 m 2 + 2 m 0 g l cos ⁡ θ δ θ + - M δ θ = 0

⇒ M δ θ = 5 m 2 + 2 m 0 g l cos ⁡ θ δ θ

⇒ M = 5 m 2 + 2 m 0 g l cos ⁡ θ

Como θ = 30 ° :

M = 5 m 2 + 2 m 0 g l cos ⁡ 30 ° = 5 m 2 + 2 m 0 g l 3 2  

⇒ M = 5 m 4 + m 0 g l 3

Resposta

M = 5 m 4 + m 0 g l 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

79- A conexão uniforme O A tem uma massa de 20k g e está apoiada no plano vertical pela mola A B cujo comprimento é de 400m m quando não está esticada. Faça um gráfico da energia potencial total V e d
78- O mecanismo articulado é usado para levantar a massa de 80k g para uma posição travada quando O B se move para O B ' na posição a 3 ° . Para avaliar a ação projetado do mecanismo, faça um gráfico
80- Determine o ângulo de equilíbrio θ para o mecanismo mostrado. A mola de rigidez k = 2 k N / m tem um comprimento de 200m m quando não está esticada. Cada uma das conexões uniformes A B e C D tem u
A prensa trabalha por meio de um mecanismo de cremalheira e pinhão, e é usada para gerar grandes forças, tais como as necessárias para produzir encaixes por pressão. Se o raio médio das engrenagens do
Determine, em função do ângulo θ , o momento M , aplicado através do eixo a conexão inferior, necessário para suportar a carga P . Despreze os pesos das partes.