Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 2

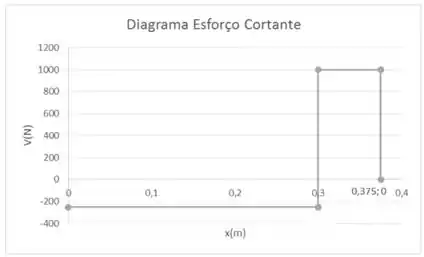
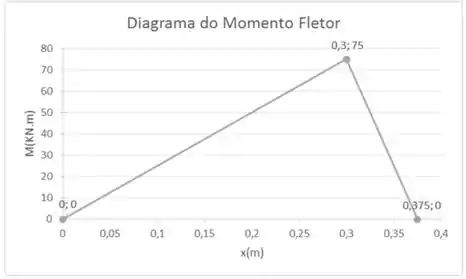
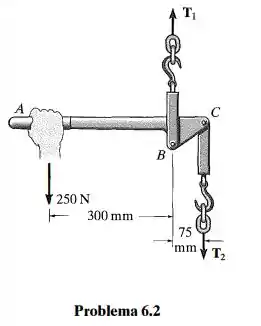
Um dispositivo é usado para suportar uma carga. Se a força aplicada ao cabo for 250 N, determine as tensões T 1 e T 2 em cada extremidade da corrente e, então, represente graficamente os diagramas de força cortante e momento fletor para o braço ABC.

Passo 1

Fala! Queremos achar esses T ' s e depois fazer os diagramas de esforços cortante e momento.

Começamos gerando um diagrama de corpo livre:

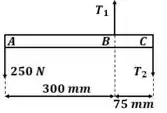
E calculamos as reações em B e C:

∑ M C = 0 ⇒ 250 ⋅ 375 - T 1 ⋅ 75 = 0

T 1 = 250 ⋅ 375 75

T 1 = 250 ⋅ 375 75

T 1 = 1250   N

∑ F y = 0 ⇒ - 250 + T 1 - T 2 = 0

- 250 + 1250 - T 2 = 0

T 2 = 1000   N

A primeira parte a gente já conseguiu!

Passo 2

Agora é fazer os diagramas. Vamos achar as equações de momento fletor e cortante.

Vamos dividir nossa viga em seções. Nossos pontos críticos serão onde começa temos forças concentradas. Teremos então duas seções. AB e BC.

Para cada intervalo, a gente corta a viga numa seção genérica distanciada x da origem estabelecida por nós mesmos e olha só para a esquerda desse corte.

O próximo passo é achar as equações do cortante e do momento para as diferentes seções. Aí é colocar as representações dos esforços com convenção positiva dentro da nossa seção e usar as equações de equilíbrio para achar os valores desses esforços.

Seção AB 0 ≤ x < 0,3   m

∑ F y = 0 ⇒ - V x - 250 = 0

V x = - 250   N

∑ M   = 0 ⇒ M x + 250 ⋅ x = 0

M x = - 250 ⋅ x       N ⋅ m

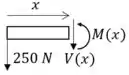
Seção AC 0,3 ≤ x ≤ 0,375   m

∑ F y = 0 ⇒ - V x - 250 + 1250 = 0

V x = - 1000   N

∑ M   = 0 ⇒ M x + 250 ⋅ x - 1250 ⋅ ( x - 0,3 ) = 0

M x = 1000 x - 375       N ⋅ m

Passo 3

V x =   - 250   N 0 ≤ x < 0,3   m - 1000   N 0,3   m ≤ x ≤ 0,375   m

M x =   - 250 ⋅ x 0 ≤ x < 0,3   m 1000 x - 375 0,3   m ≤ x ≤ 0,375   m

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pino liso está apoiado em duas chapas A e B e sujeito a uma carga de compressão de 0,4k N / m provocada pela barra C . Determine a intensidade da carga distribuída w 0 das chapas agindo sobre o pino
Represente graficamente os diagramas de força cortante e momento fletor para a viga de madeira e determine a força cortante e o momento fletor em todo o comprimento da viga em função de x .
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento em função de x .
Determine o torque resultante interno que age sobre as seções transversais nos pontos C e D do eixo. O eixo está preso em B.