Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 72
O mastro de tem uma massa de e tem centro de massa na metade do seu comprimento. Ele é apoiado por uma rótula em e pelos dois cabos sob forças trativas e . O cabo que suporta a carga de passa por uma polia em e é preso ao plano vertical - em . Calcule o módulo da força trativa . (Sugestão: Escreva uma equação para o momento que elimina todas as incógnitas exceto ).
Passo 1
Primeiro precisamos representar as forças envolvidas no sistema. Isso inclui os pesos do mastro e da carga, as trações nos cabos e a força normal de reação em :
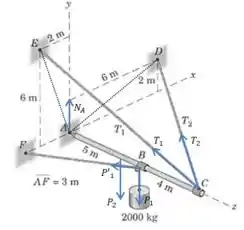
Agora vamos seguir a sugestão do enunciado, temos que escolher algum eixo de referência para calcularmos o momento de forma que todas as incógnitas, exceto , desapareçam da equação.
Essas incógnitas desconhecidas são e . As linhas de ação dessas forças passam pelos pontos e , respectivamente. Então vamos calcular o momento em relação ao eixo , que já está representado por uma linha pontilhada no desenho.
E para projetar os momentos nesse eixo vamos precisar do vetor unitário na direção :
Passo 2
Beleza, agora vamos escrever as forças que sobraram em forma vetorial:
E para escrever vamos precisar do vetor unitário na direção :
Ok, e vamos precisar também dos vetores que dão a posição entre o eixo e o ponto onde cada força é aplicada. Por simplicidade, vamos tomar todos os vetores a partir do ponto do eixo :
Passo 3
E então o momento em relação ao eixo pode ser calculado usando a fórmula:
E sabemos que esse momento é nulo, porque o sistema está em equilíbrio. Vamos resolver primeiro os produtos vetoriais:
E agora vamos pegar cada um desses resultados e fazer o produto escalar pelo vetor , e substituir e .
Agora é só substituir na equação de equilíbrio:
Resolvido!
Resposta
A força é .