Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 63

Um bloco retangular uniforme de altura h e massa m está centrado em uma posição horizontal, sobre a superfície circular fixa de raio r . Determine o valor limite de h para haver estabilidade.

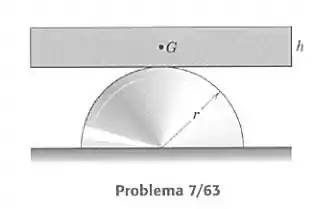
Passo 1

Se o sistema está em equilíbrio, ao girarmos bloco de um ângulo pequeno δ θ , devemos ter uma variação da energia potencial do sistema igual a zero:

δ V δ θ = 0

Além disso, se a segunda derivada da função potencial for positiva, o equilíbrio será estável:

δ 2 V δ θ 2 > 0 → E q u i l í b r i o   e s t á v e l

Então, vamos calcular a variação da energia potencial gravitacional relacionada com h , e tentar satisfazer a condição de equilíbrio estável.

Passo 2

Vamos desenhar o bloco inclinado de um ângulo θ em relação à vertical, e tentar calcular a altura y o seu centro de massa.

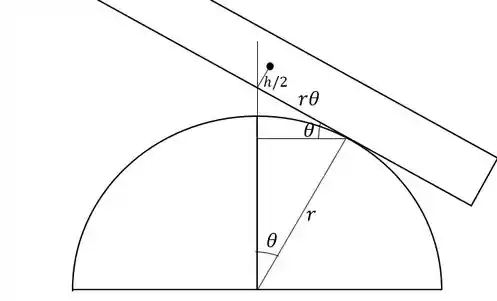
Como vemos na figura, a altura do centro de massa em função de θ é:

y = r cos ⁡ θ + r θ sen ⁡ θ + h 2 cos ⁡ θ

Derivando, obtemos a veriação δ y da altura em função da variação δ θ :

δ y = - r sen ⁡ θ + r sen ⁡ θ + r θ cos ⁡ θ - h 2 sen ⁡ θ δ θ = r θ cos ⁡ θ - h 2 sen ⁡ θ δ θ

Então temos a variação da energia potencial:

δ V = m g δ y = m g r θ cos ⁡ θ - h 2 sen ⁡ θ δ θ

Passo 3

Já temos a derivada da função potencial:

δ V δ θ = m g r θ cos ⁡ θ - h 2 sen ⁡ θ

No nosso caso temos θ = 0 , então δ V / δ θ já é igual a zero. Falta então que δ 2 V δ θ 2 seja positivo. Derivando de novo:

δ 2 V δ θ 2 = m g r cos ⁡ θ - r θ sen ⁡ θ - h 2 cos ⁡ θ > 0

Para θ = 0 o cosseno é 1 e o seno é zero, temos então:

m g r - h 2 > 0

Cortando m g :

r - h 2 > 0

⇒ r > h 2

⇒ h < 2 r

Resposta

h < 2 r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao se testar o projeto mostrado de um macaco guiado por um fuso, 12 voltas na manivela são necessárias para elevar o pedal de 24 mm. Se uma força F = 50 N, aplicada normalmente ao eixo da manivelam é
Calcule a eficiência com a qual a cunha, com inclinação de 5°, eleva o peso W , sob a ação da força horizontal P atuando na cunha. O coeficiente de atrito entre a cunha e o bloco vale 0,30.
A plataforma de trabalho portátil é elevada por intermédio de dois cilindros hidráulicos articulados nos pontos C . Cada cilindro está sob uma pressão hidráulica p e tem uma área de pistão A . Determi
A caçamba do caminhão de entrega de alimentos para aeronaves tem massa m quando carregada e é levantada pela aplicação de um torque M na extremidade inferior da engrenagem, que é articulada com a estr
Determine o momento M que deve ser aplicado em O para sustentar o mecanismo na posição θ = 30 ° . As massas do disco em C , da barra O A e da barra B C são m 0 , m e 2 m , respectivamente.