Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 80
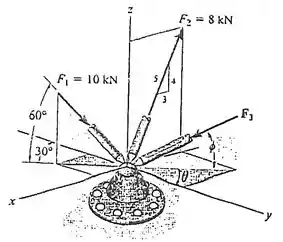
Se , e , determine a intensidade e os ângulos de direção coordenados da força resultante que atua sobre a junta esférica
Passo 1
Faaalaa!
O exercício nos dá 3 forças, suas orientações e nos pede para encontrar a resultante, vamos começar decompondo essas forças.
Para , de início já podemos encontrar a direção , dado que a força faz 6 com o plano . Como o ângulo é oposto ao eixo , multiplicamos a força por seno de para achar a componente em .
Ela ficou negativa porque a força aponta para baixo, ou seja, para o sentido negativo de .
Já a projeção no plano vamos achar multiplicando a força por cosseno
Com a projeção da força nesse plano a gente consegue achar as componentes e . E então decompomos em e , sabendo que a projeção faz com o eixo , vamos achar a componente em usando cosseno e em usando seno desse ângulo
Temos em
Negativo porque ela aponta para a parte negativa de .
E temos em :
Essa é positiva porque a força aponta para o sentido positivo de .
Assim, o vetor cartesiano de fica:
Passo 2
Vamos para a , ela está contida plano , então terá duas componentes, enquanto a componente zera. Vamos encontra-las usando a relação de catetos e hipotenusas do triângulo dado:
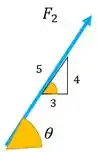
No eixo
No eixo :
Essa última é negativa porque nosso vetor aponta para a parte negativa de .
Logo, nossa como vetor cartesiano fica:
Passo 3
Para o , com as informações dadas no enunciado podemos encontrar a direção , dado que a força faz com o plano . Assim esse ângulo é oposto ao eixo , por isso usamos seno
Fica negativo porque essa força aponta para baixo.
Já a projeção no plano é dada por:
E então decompomos em e , sabendo que a projeção faz com o eixo :
Temos em
E temos em :
Ela aponta para o sentido negativo de , por isso o sinal de menos.
Caso estivesse apontando no sentido que estamos acostumados o vetor teria negativo, positivo e positivo, já que está com sentido oposto colocamos as componentes opostas, assim, o vetor cartesiano de fica:
Passo 4
Podemos agora encontrar nossa força resultante. Vamos somar cada componente separadamente:
Obtemos então:
E a intensidade do seu módulo será:
Passo 5
Só falta encontrar os ângulos de direção coordenados de , usando a fórmulinha deles:
Então: