Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 62
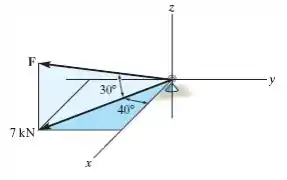
Determine a intensidade e os ângulos diretores coordenados da força F que atua sobre o suporte. A componente de F no plano x–y é 7kN.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como está com essa pandemia?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a força a partir do eixo. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar como fazer a força resultante pela decomposição das forças pelo ângulo.
A gente vai precisar decompor as outras 3, certo??
Já temos meio passo andado, ainda precisamos calcular o eixo z.
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e achar nossos valores!!